les brenoms en questions
Quelques sujets de réflexion, présentés par Pierre Duchet, à partir de textes de synthèse écrits par les collégien(ne)s au cours de leur recherche. Ces questions peuvent servir de point de départ pour des activités de recherche intéressantes permettant des apprentissages numériques, logiques et algébriques importants (abordables dès la 6ème, utiles en terminale et au delà).
Quelles divisions sont possibles chez les brenoms ?
La division de brenoms se fait comme la multiplication à trous. Ainsi
… 0 0 0 7 |… 0 0 0 3
|
revient à faire
… 0 0 0 3
× ?
… 0 0 0 7
Certaines divisions sont impossibles, ainsi lorsque que le dividende est impair et le diviseur pair. Exemple …17 : …4 = ?.
Démonstration :
tous les multiples de 4 se terminent par un chiffre pair, donc il est impossible de
trouver un brenom x tel que …4 × x = …17.
Un curieux phénomène ?
Nous avons remarqué que
… 0 0 7
…7 1 4 2 8 6 ×
… 4 2
… 5 6
… 1 4
… 2 8
… 0 7
… 9
………………
… 0 0 0 0 2 =
Donc … 0 0 2 : … 0 0 7 = … 7 1 4 2 8 6.
Si nous faisons à la calculatrice 2 : 7, nous obtenons 0,28571428, un nombre dont les
décimales ont pour période 285714. Or :
… 2 8 5 7 1 4
…7 1 4 2 8 6 +
… 0 0 0 0 0 0 =
Nous avons constaté cela sur plusieurs autres résultats de division, mais nous ne savons pas l’expliquer.
1 a t-il plusieurs racines carrées ?
Nous cherchons les brenoms x tels que x × x = 1,
autrement dit les brenoms dont le carré est 1, les “racines carrées de 1” en
quelque sorte (nous écrivons 1 pour simplifier l’écriture de … 0 0 0 1).
[NDLR : Une écriture du type x × x = 1 est une équation et amène la question : puis-je
remplacer x par quelque chose de mieux connu pour que l’équation soit juste ? Ces
objets mieux connus, s’il existent sont appelés les solutions de l’équation.
Résoudre une équation, c’est parvenir à connaître toutes les solutions d’une
équation. Notre problème ici est de résoudre l’équation x × x = 1 chez les
brenoms.]
Bien évidemment, il y a la solution
… 0 0 0 1 × … 0 0 0 1 = … 0 0 0 1 = 1
Y en a-t-il d’autres ? Si nous ne regardons que les premiers (de droite à gauche) chiffres pour faire une table de multiplication de … a × … a, nous voyons que 1 et 9 sont les seuls premiers chiffres possibles d’un brenom dont le carré est 1.
Essayons avec 9 :
cherchons le 2ème chiffre possible d’un brenom x commençant (à
droite) par 9 et tel que x × x = 1. En regardant les deux premiers chiffres des
multiplications possibles, on s’aperçoit que le 2ème chiffre ne peut
être que 4 ou 9.
Première piste : le brenom périodique … 9 9 9 semble être une solution. Nous avons
prouvé que les 10 premiers chiffres de la multiplication … 9 9 9 × … 9 9 9
étaient bien 0 0 0 0 0 0 0 0 0 1. Nous n’avons pas encore réussi à prouver que les
chiffres suivants sont toujours des 0.
Conjecture 1 : … 9 9 9 9 × … 9 9 9 9 = 1.
[NDLR : Une conjecture est une propriété que l’on pense vraie, mais que l’on n’est pas parvenu à démontrer : on ne peut donc être certain que c’est vrai.]
Deuxième piste : poursuivons la recherche d’une solution du type … 4 9 . Appelons c le troisième chiffre et effectuons la multiplication (les retenues sont comptabilisées, mais seul le premier chiffre, à droite, des nombres calculés nous intéresse : nous avons écrit entre parenthèses le résultat des calculs pour dire que ne n’en retenons que le premier chiffre) :
… c 4 9
… c 4 9 ×
…(9c+4) 4 1
…… 9 6
… (9c)……
…(18c+14) 0 1 =
Donc le nombre 18 c + 14 doit se terminer par 0. Or 18 c + 14 se termine par le même chiffre que 18 c + 4, et 18 c + 4 se termine par le même chiffre que 8 c + 4. Si le nombre 8 c + 4 se termine par 0, alors 8 c se termine par 6. Il y a deux solutions 8 × 2 = 16 et 8 × 7 = 56 donc deux brenoms possibles … 2 4 9 ou … 7 4 9.
Premier essai :
c = 7. Appelons d le chiffre suivant (c’est le 4ème). En calculant comme précédemment le 4ème chiffre de
… d 7 4 5 × … d 7 4 5,
on trouve que c’est le dernier chiffre de 18 d + 24, donc de 18 d + 4, donc de 8 d + 4. Si 8 d + 4 se termine par 0 alors 8 d se termine par 9. C’est impossible : on voit qu’il n’y a aucune solution à notre équation qui commence par … 7 4 9.
Deuxième essai :
c = 2. En procédant comme ci-dessus, on trouve que 8 d doit se terminer par 8. Il y a deux brenoms possibles …6 2 4 9 ou …1 2 4 9.
Conclusion :
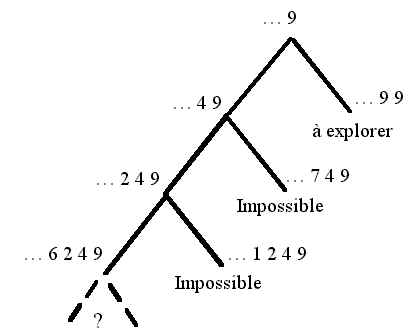
nous avons poursuivi nos explorations pour le 5ème, pour le 6ème chiffre, … A chaque fois, il y a 2 valeurs possibles pour le chiffre cherché ce qui conduit à deux essais pour le chiffre suivant, deux branches d’exploration. L’une des branches meurt : il n’y a aucune possibilité pour le chiffre suivant. L’autre branche se poursuit pour donner naissance à deux autres branches, dont l’une, à son tour, va mourir, etc … Il semble donc finalement qu’il y ait un brenom (et un seul) qui soit solution de notre équation x × x = 1, qui commence par 9 et qui soit différent de …999, mais nous ne savons pas encore trouver tous ses chiffres.

Conjecture 2 : Il y a un brenom et un seul qui commence par 9 qui est différent de …999 et dont le carré est 1.
Il reste aussi bien sûr à explorer la question de l’existence d’une solution commençant par 1 et différente de … 0 0 0 1.
racine carrée (notes d'une élève)