Comptes Rendus MATh.en.JEANS 00-01

(1) élève de 4ème au collège L'Ardillière de Nézant à St Brice (Val d'Oise).
(2) élève de 3ème au collège Charles Lebrun à Montmorency (Val d'Oise).

Jumelage MATh.en.JEANS entre les collèges Charles Lebrun à Montmorency et L'Ardillière de Nézant à St Brice (Val d'Oise).
Enseignants : Yann BOURIT, (St-Brice) et Christian GEORGES (Montmorency).
Chercheur : Gilles CHRISTOL, professeur et chercheur en Mathématiques à l'université Paris VI.

Introduction

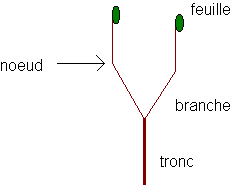
Un arbre comprend : un tronc, des noeuds, des branches, et des feuilles.

Le problème est de compter les arbres qui ont un nombre donné de branches, et de donner une méthode permettant de les dessiner tous une fois et une seule.

Avant de vous expliquer ce que nous avons fait, nous allons tout d'abord vous donner quelques définitions importantes qui vous seront utiles:

A(b), c'est le nombre d'arbres à b branches

ex: A(5) est le nombre d'arbres à 5 branches.

B(b), c'est l'ensemble des arbres à b branches. ex: B(2)

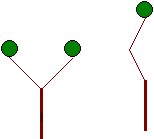
Une tige, c'est la suite de branches qui part du tronc et qui se finit par une feuille.

ex: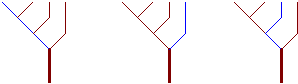

1. Au commencement de nos travaux

Pour commencer, nous avons voulu dessiner tous les arbres à 1, puis à 2, puis à 3 branches. Cela est vite devenu trop difficile. Mais nous avons trouvé quelques solutions et ceci nous a mis sur la piste de "the" solution.

nous avons constaté que :

A(2) = A(1) + A(1)

A(3) = A(2) + A(2)

Mais, à partir de là :

A(4) = A(3) + A(3) + quelquechose

A(5) = A(4) + A(4) + quelquechose

etc...

C'est en cherchant à expliquer ce phénomène que nous avons trouvé la bonne piste.

Nous pouvons l'expliquer en faisant des catégories:

• les Béberts : ils n'ont qu'une branche qui part du tronc. On greffe B(b) au-dessus de cette branche.
• les Djerkys : ils ont une branche qui part du tronc. On greffe B(b) à côté de cette branche.
• les Porkys : c'est le reste...

exemple : les arbres à 5 branches

B(5) est formé de Béberts et de Djerkys sur chacun desquels on greffe B(4). Cela donne:

A(5) = A(4) + A(4) + les porkys à 5 branches

Nous pouvons généraliser:

A(b) = A(b-1) + A(b-1) + les porkys à (b-1) branches

2. Comment trouver le reste: les Porkys

les Porkys ne sont ni des Béberts, ni des Djerkys. ce sont donc des arbres qui ont au minimum 2 branches au premier étage et qui n'ont aucune tige de longueur 1.

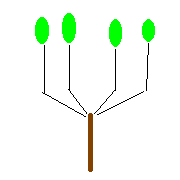
on prend pour exemple les Porkys à 8 branches.

Nous allons faire des sous-catégories selon le nombre de branches qui partent du tronc.

• Puisqu'on ne doit pas avoir de tiges de longueur 1, on ne peut pas avoir plus de 4 branches au premier étage : il n'y a qu'un arbre à 4 tiges de 2 branches.

le chandelier à 4 tiges

• On met moins de branches sur le tronc, c'est à dire 3.
• On distribue les 5 branches restantes (8-3),il n'y a que 2 partitions possibles, cela nous donne:

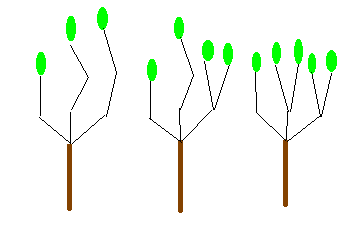
a) 5 = 1+1+3   il y  a  A(3) arbres possibles, c'est à dire 4.
b) 5 = 1+2+2  il y en a 3

• Il reste ceux qui ont 2 branches au premier étage. On distribue les 6 branches restantes (8-2), cela nous donne:

a) 6 = 1+5

il y en a A(5), c'est à dire 20

b) 6 = 2+4

A(2)xA(4) = 2x9 = 18

Il y en a 18.

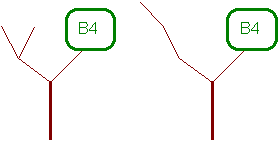c) 6 = 3+3 : attention symètrie !

Comme on va greffer deux arbres à trois branches sur chaque tige, il faut faire attention à ne pas compter deux fois les mêmes, car l'arbre "ab" est le même que l'arbre "ba" (voir schéma).

Explications:

Si on nomme a, b, c et d les 4 arbres à 3 branches et qu'on les greffe au-dessus des deux branches du 1er étage:

a d

a c        b d

a b        b c       c d

a a        b b       c c         d d

\/           \/           \/           \/

on obtient 4+3+2+1 = 10 arbres différents.

Il y a une formule pour faire ce genre de calculs : c'est [A(3)x(A(3)+1)]:2

En fin de compte nous avons trouvé :

10+18+20+3+4+1=56

Il y a 56 Porkys à 8 branches. On leur ajoute  2x115 (les djerkys et les béberts), et on obtient 286 arbres à 8 branches.

3. "THE SOLUTION"

a) On définit le nombre de branches au 1° étage ( il est plus pratique de partir du nombre le plus élevé et de décroître), on calcule le nombre des branches restantes et on décompose ce nombre en autant de termes que de branches au 1° étage.

exemple : on considère un arbre à 9 branches ayant 3 branches au 1° étage.

9-3 = 6

il nous reste 6 branches à décomposer en une somme de 3 termes, puisqu'il y a 3 branches au 1er étage.

6 = 4+1+1

6 = 3+2+1

6 = 2+2+2

b) On convertit ces termes en A(b) et on remplace les "+" par des "x".

ex : 6 = 4+1+1 devient A(4)xA(1)xA(1) = 9x1x1 = 9

      6 = 3+2+1 devient A(3)xA(2)xA(1) = 4x2x1 = 8

c) Cas particulier

Quand on a 3 termes identiques, pour ne pas compter 2 fois le même arbre ( problème de symétrie vu plus haut), on utilise la formule ci-dessous :

exemple : 6 = 2+2+2  devient  [A(2)x(A(2)+1)x(A(2)+2)]:6

  En résumé:

• quand les nombres de la partition sont tous différents, on multiplie entre eux les A(b) de chaque terme.
• quand 2 nombres de la partition sont identiques, on fait:[A(b)x(A(b)+1)]:2
• quand 3 termes de la partition sont identiques, on fait:[A(b)x(A(b)+1)x(A(b)+2)]:6
• quand 4 nombres de la partition sont identiques, on fait [A(b)x(A(b)+1)x(A(b)+2)x(A(b)+3)]:24

remarque : (nous n'avons pas eu le temps de nous pencher sur le rapport entre chaque dénominateur, mais notre professeur nous a dit que c'était des "factoriels")

• Et quand il y a deux nombres égaux mélangés avec d'autres nombres (exemple : 7=2+2+3), on calcule [A(2)x(A(2)+1)]:2  (pour les 2+2) et on multiplie par A(3) (pour le 3).

  Grâce à cette méthode, voici les résultats que nous avons trouvés:

Il faut dire que la consultation du site ci dessous nous a aidés à corriger quelques calculs.

http://www.research.att.com/~njas/

C'est un site où sont répertoriées toutes les suites connues à ce jour, et M. SLOANE est très aimable et très serviable.

[le lien est périmé - voir la page sur Neil Sloane dans Wikipedia et le site de l'OEIS]

Le défaut de notre méthode, c'est que, si on se trompe dans un calcul, tous les suivants sont faux aussi.

Comptes Rendus MATh.en.JEANS 00-01

© MATh.en.JEANS 2001. Tous droits réservés.