par GUNDAG Rakibe, RIVALLAN Estelle, SANTHIRALINGAM Samantika,élèves des lycées R.Rolland d’Argenteuil et P. Eluard de Saint-Denis

Professeurs : BRUN Olivier ; DESESPRINGALLE Franck ; GUY Dominique ; HUET Alain

Chercheur : ALLYS Loïc

Un professeur de mathématiques qui s’appelle François va en Turquie et échange mille francs contre un tas de pièces. Un jour de pluie, François ne peut pas sortir et reste donc dans sa chambre avec son amie Olive. Ils s’ennuient tellement qu’ils décident d’essayer de trouver un sujet de contrôle pour leurs élèves de première scientifique qui étudient les probabilités. Pour cela, Olive a eu une idée lorsqu’elle a vu toutes ces pièces turques. Elle a pensé qu’il y avait peut-être (et au maximum) une fausse pièce qui pouvait être soit plus lourde, soit plus légère que les autres. François et Olive disposent d’une pièce étalon (c’est-à-dire une vraie pièce) et d’une balance à plateaux pour trouver en un minimum de pesées cette éventuelle fausse pièce.

n : nombre de pièces

k : nombre de pesées

E : pièce étalon

1,2,3… : le numéro de la pièce

(…) ­ (…) : la balance à plateaux

= : équilibre de la balance

¹ : déséquilibre de la balance

Olive : Si on essayait d’abord de trouver cette fausse pièce (s’il y en a une) sans utiliser la pièce étalon ?

François : Je veux bien à partir de 3 pièces mais pour 1 et 2 pièces, ce n’est pas possible : nous devons utiliser la pièce étalon. Regarde !

Avec 1 pièce : 2 cas

1^er cas : ( 1 ) = ( E ) Þ il n’y a pas de fausse pièce

2^e cas : ( 1 ) ¹ ( E ) Þ la "1" est fausse

Avec 2 pièces : 2 cas

:

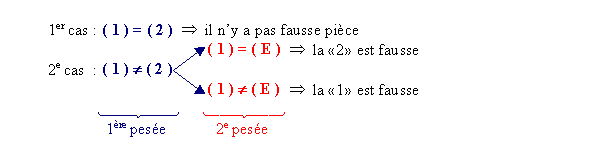François : Tu vois, on est obligé d’utiliser la pièce étalon lors de la deuxième pesée.

Olive : Essaye avec 3 pièces.

François : D’accord. Regarde ce que l’on trouve sans la pièce étalon.

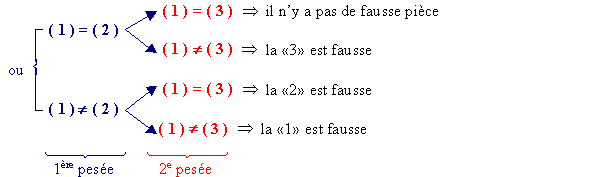
Au bout d’une demi-heure, François et Olive avaient déjà trouvé le nombre de pesées qu’il fallait pour 3 pièces, 4 pièces…9 pièces. Voici le tableau des résultats :

François : J’ai fait une conjecture ! (C’est-à-dire, j’ai deviné une loi)

 

Quand n ³ 3 et n pair,(cela marche aussi pour n = 2 mais il faut utiliser la pièce étalon donc on ne prend pas ce cas en compte)on a :

      k étant le nombre de pesées suffisant

Quand n ³ 3 et n impair, (cela marche aussi pour n = 1 mais on ne prend pas ce cas en compte pour la même raison que précédemment) on a :

k étant le nombre de pesées suffisant

 

 

Olive : Nous pouvons utiliser une autre méthode : la dichotomie. Pour ce faire, prenons pour nombre de pièces dans chaque plateau une puissance de 2. Regarde avec 4 et 9 pièces ce que l’on trouve !

François : pour 9, on laisse une pièce de côté et on met 4 pièces sur chaque plateau. Si la pièce laissée est fausse, la balance sera équilibrée.

Avec 4 pièces : il faut 3 pesées :

Avec 4 pièces : il faut 3 pesées ( 1,2 ) = ( 3,4 ) Þ il n’y a pas de fausse pièce

 

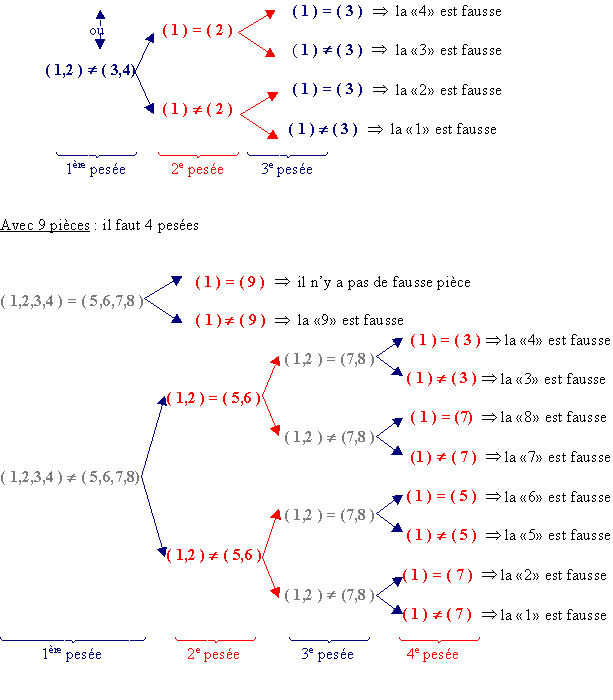
De façon analogue, François et Olive ont obtenu les résultats suivants :

4.5.6.7

Olive : Moi aussi j’ai une conjecture

Si n est le nombre de pièces et k l'exposant de 2, alors et le nombre suffisant de pesées est alors k.

 

François : Regarde Olive ! Pour 12 pièces, on peut trouver la fausse pièce, avec la pièce étalon, en 3 pesées alors qu’il t’en a fallu 4

.

 

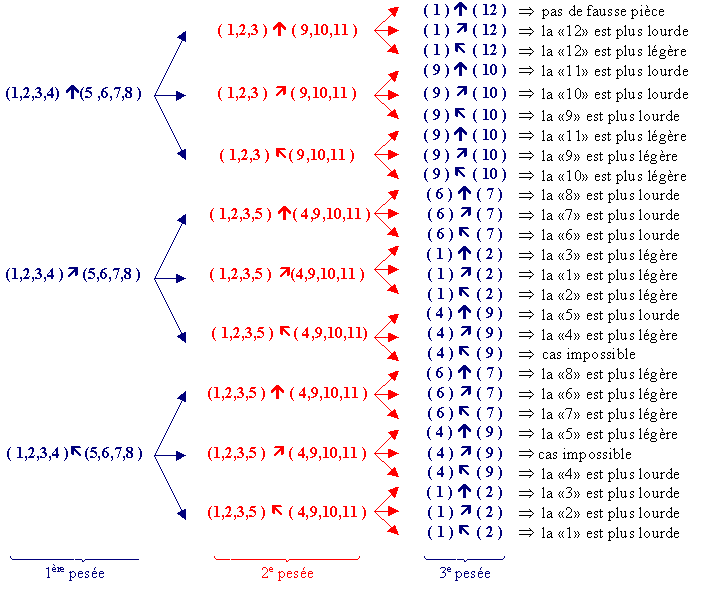
Olive : C’est vrai, nous n’avions pas tenu compte d’une information ! Nous ne savions pas si la fausse pièce était plus lourde ou plus légère que les autres. De plus, nous n’avons pas utilisé la pièce étalon et l’exemple de 12 pièces nous laisse supposer qu’elle permet de trouver la fausse pièce plus rapidement.

 

 

IV AVEC UNE PIECE ETALON

Olive : Si nous avons n pièces, il y a 3 possibilités :

ï soit toutes les pièces sont bonnes : 1 cas

ï soit une pièce est plus lourde que les autres : n cas

ï soit une pièce est plus légère que les autres : n cas

Nous avons donc 2n + 1 cas différents.

François : De plus : pour la 1^ère pesée, on a 3 résultats possibles

pour la 2^e pesée, on a 3² résultats possibles

pour la pesée numéro k, il y a 3^k résultats possibles

---

voir le schéma suivant

(1) (2) (3)

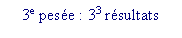
(1)

(2)

(3)

 

c’est le maximum de résultats possibles (car dans le schéma précédent, on compte des cas impossibles)

donc 2n + 1 £ 3^k

Olive : Si on s’intéressait au cas où 2n + 1 =

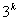
2n + 1 = Û

Grâce à cette égalité, j’ai établi le tableau suivant :

François : Avec k pesées, on peut connaître au plus pièces, avec :

N_k = Û 2N_k + 1 =

 

Démontrons, par récurrence seule, que N_k+1 = 3N_k + 1, on note cette propriété (P_k)

ï pour k = 0, N₀ = 0 et N₁ = 1

donc on a bien N₁ = 3N₀ + 1 Þ (P₀) est vraie

 

ï supposons, pour un k donné, que N_k+1 = 3N_k + 1

N_k+1 = donc 3N_k+1 + 1 = 3* + 1

donc 3N_k+1 + 1 = + 1

or, 3^k+2 = 2N_k+2 +1

d’où 3N_k+1 + 1 =

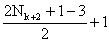
3N_k+1 + 1= N_k+2 – 1 + 1

3N_k+1 + 1= N_k+2

 

donc si (P_k) est vraie, alors (P_k+1) est vraie.

 

Conclusion : La propriété (P₀) est vraie. Si elle est vraie pour k, alors elle vraie pour k+1. Donc elle est vraie pour tout k Î IN. Donc, si avec k pesées on connaît le nombre de pièces maximum que l’on peut déterminer, alors on peut connaître le nombre de pièces maximum que l’on peut déterminer avec une pesée supplémentaire.

 

Olive : Je pense que tes élèves voudront une exercice beaucoup plus facile et qu’ils pourront faire en une heure, non pas en trois jours.