Comptes Rendus MATh.en.JEANS 00-10

Jeu de poursuite sur un échiquier

Jumelage MATh.en.JEANS entre le lycée Polyvalent Frédéric Joliot Curie (Atelier Scientifique) de Dammarie-lès-Lys (77) et le lycée Moissan de Meaux (77), année scolaire 1999-2000.
Enseignants : Mme Sandrine Dubois, M. Guillaume Davodeau (lycée Curie) et Mme Sandrine Lefranc (lycée Moissan)
Chercheur : Olivier Bodini (Equipe Combinatoire, Paris)

---

[Article vérifié et commenté : les passages entre crochets sont des éditeurs]

Plan   [Seule une version préliminaire de l'article nous étant parvenue, nous avons réorganisé diverses parties du manuscrit.]

1. [Le problème]
2. Exemples élémentaires
3. Cadre mathématique
4. Stratégies [du joueur B]
5. Conclusion et ouverture : [généralisations et question ouvertes]

1. [Le problème]

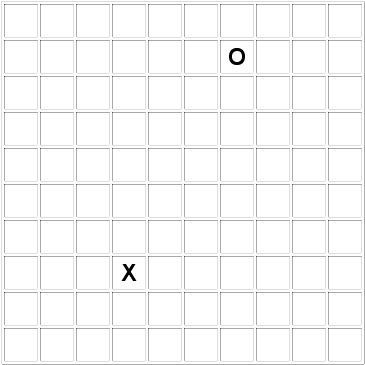
Règles Par le biais d'un échiquier [carré] de dimension n, deux joueurs s'affrontent de la façon suivante : Le premier L'un, nommé B,  possède un ballon et est symbolisé par un pion O (le défenseur). Le deuxième L'autre, nommé A, possède plusieurs pions symbolisés par X (l'attaquant). A  joue en premier, il se déplace comme un roi aux échecs, son objectif est de prendre la balle à B  en se plaçant sur la même case que celui-ci. B  se déplace de la même manière et a pour objectif de ne pas se faire prendre. On s'est proposé de répondre à la question suivante :   Combien faut-il au minimum d'attaquant(s) pour prendre la balle au défenseur ?

Figure 1

D'après notre étude il ne faut qu' il suffit d'un seul attaquant pour mettre en échec le défenseur (remarque : on suppose que chaque joueur joue au mieux, c'est à dire les coups les mieux adaptés à la situation).

2. Exemples élémentaires

Cas n=3

Cas n=4

Problématique.
Nous allons tenter de généraliser au cas nx n. Sur un échiquier quelconque le défenseur est-il toujours en échec ?

3. Cadre mathématique

Distance

On suppose qu'un déplacement diagonal compte autant qu'un déplacement vertical ou horizontal (Figure 5).   Définition. Distance entre deux positions des joueurs A et B : c'est le nombre de déplacements minimum pour que A atteigne B. [Si A et  B désignent les positions des joueurs, la distance est notée :] d( A;B) Pour l'exemple de la Figure 6, on a d( A;B)=3.

Figure 5 Figure 6

Distance au n^ème coup : d( A_n;B_n) 

C'est, [au  n^ème coup,] le nombre de déplacements minimum pour que A atteigne B : A_n est la position de A au  n^ème coup ; B_n est la position de B au n^ème coup.

Propriétés [relatives à cette distance]

d( A;B) = max (L,l) En prenant appui sur [les positions] A et B, on peut construire un rectangle de côtés L et  l  (éventuellement plat [Lou l nul ], quand A et B sont soit sur la même ligne soit sur la même colonne). Dans l'exemple de la Figure 7, on a L=6, l=4 et d( A;B) = max ( L,l) = 6.

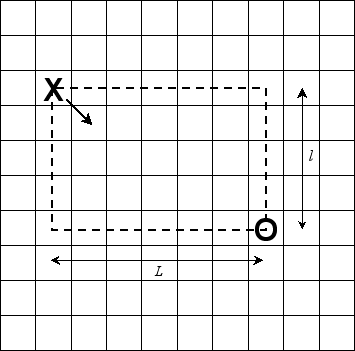Figure 7

Peut-on toujours garder une distance constante ?

Comme A joue au mieux, il va se rapprocher de B, [...] Si  B n'est pas au bord et en jouant bien, on a :   Théorème 1 [Si A joue bien], d( An+1,Bn) d( An,Bn) -1 .   [Ce «théorème» est à vrai dire, une définition de l'expression «jouer bien» pour le joueur A]. Pour bien jouer, A [lorsque c'est à lui de jouer] se rapproche de B, donc il diminue sa distance de 1 au  n+1ème coup [...] (voir l'exemple de la Figure 8).

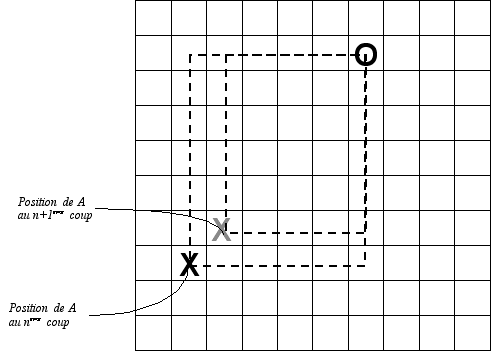Figure 8

Selon le jeu de B la distance entre les deux pions peut-être constante ou diminuée.

Théorème 2. Si A joue bien et quoi que fasse B, on a : d( An+1,Bn+1) d( An,Bn) .

Démonstration. D'après l'inégalité triangulaire d( An+1,Bn+1) d( An+1;Bn) + d( Bn;Bn+1), [d'où :]  d( An+1,Bn+1) d( An,Bn) -1 +1 , d'après le théorème précédent.

4. Stratégies [du joueur B]

Deux stratégies sont possibles pour que B garde une distance constante par rapport à A : la fuite ou la spirale. La fuite. Mais l'échiquier à des dimensions finies, B est alors toujours poussé vers un bord. La spirale. B ne peut pas tourner autour de A car l'échiquier étant fini, B au bout d'un certain temps ne peut plus garder une distance constante. Quand A va se trouver dans la même ligne ou même colonne que B, A n'aura plus qu'à suivre la même trajectoire que B et le coincer dans un bord.   [Remarque des éditeurs : faute de précisions suffisantes sur les deux stratégies envisagées, les affirmations et arguments précédents ne peuvent être ni vérifiés ni démentis. Cela ne gêne en rien les raisonnements présentés dans la suite, qui tiendront compte de toutes les possibilités dans le jeu de B.]

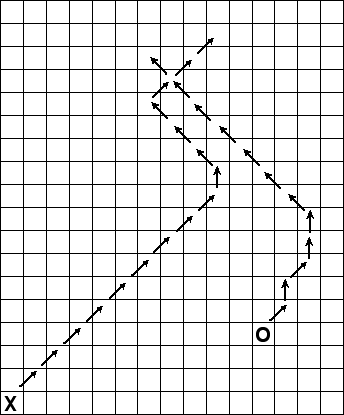Figure 9

On a le résultat suivant :

[Théorème ou conjecture 3 : voir note 1] Lemme de rapprochement
[Quelle que soit la manière de jouer de B], il existe, [si A joue bien,] un rang  n_o tel que

Démonstration [à compléter : voir note 1]

A un certain rang no, B se trouve au bord de l'échiquier [voir note 1], on a : (voir l'exemple de la Figure 10 :[en grisé, les positions après le no-ème coup, en noir celles après le (no+1)-ème coup]). Au (no+1)-ème coup, on a : [Ceci est bien la conclusion voulue, mais le raisonnement s'est appuyé sur l'exemple de la figure, dans lequel Lo lo . Il convient de compléter la preuve dans les cas où lo est supérieur à Lo, voir note 2].

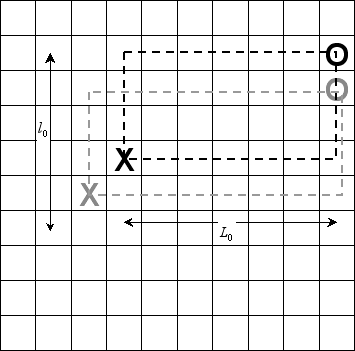Figure 10

On a démontré qu'une fois au bord la distance diminue de 1. En allant d'un bord à l'autre on finit toujours par attraper le défenseur [voir note 3].

Conclusion :

Théorème 4. [On suppose vrai le lemme de rapprochement]

Il suffit d'un seul attaquant pour mettre en échec le défenseur, et ce quelle que soit les dimensions finies de l'échiquier. 

5. Conclusion et ouverture :[généralisations et questions ouvertes]

1. Cas d'un échiquier de dimension  nx p ( p< n). [Il] se ramène [facilement à celui de] l' échiquier [carré] nx n.
2. Cas ou l'échiquier serait un cube (cas étudié par le lycée Moissan à Meaux [note 4])
3. Cas où les déplacements de B seraient supérieurs à ceux de A. Par exemple B fait 2 [pas par déplacement , alors que] A n'en fait que 1.
4. Cas où les déplacements de A seraient limités ( [à des pas] horizontaux et verticaux par exemple).
5. Cas d'un échiquier de dimension infinie : il faudrait sans doute plusieurs attaquants pour tenter de mettre en échec le défenseur.
6. Cas où l'on mettrait plus d'attaquants pour réduire le nombre de coups à jouer [pour mettre en échec le défenseur].
   [...]

1. Le schéma de la preuve proposée comporte deux parties.

(1) soit, à un certain moment de la partie, le distance entre A et B diminue (1ère éventualité), soit la distance de B au bord de l'échiquier diminue (2ème éventualité).
(2) Si la seconde éventualité se produit, alors la première se produit aussi.

Dans leur texte, les auteurs réduisent la justification de (1) à l'affirmation :

« à un certain rang n₀, B se trouve au bord de l'échiquier »

sous l'hypothèse, implicite, que la distance de A à B n'a pas diminuée (ce qui, vu l'inégalité du théorème 1, revient à dire que B joue à chaque fois de manière à augmenter d'une unité sa distance à la position précédente de A). Mais la validité de cette affirmation n'est pas évidente ; par exemple l'énoncé suivant

" Si d( A_n+1,B_n+1)= d( A_n,B_n), alors à son n+1^ème coup, B s'est rapproché du bord. "

est faux.

On peut espérer qu'une légère modification de cet énoncé est vraie, ce qui fournirait la démonstration manquante pour (1) : il suffirait de trouver un morceau M du bord, déterminé une fois pour toute, pour lequel on aurait l'implication suivante :

"Si d( A_n+1,B_n+1)= d( A_n,B_n), alors à son n+1^ème coup, B s'est rapproché de M."

retour au texte

2. On pourrait sans doute montrer que dans le cas où l_o est supérieur à L_o, et si la distance de A à B ne diminue pas, B se rapproche d'un coin de l'échiquier. Lorsque B atteint ce coin, il ne peut plus s'éloigner de la position courante de A.

retour au texte

3. Il suffit de considérer la nouvelle position obtenue comme le début d'une nouvelle partie, à laquelle s'applique alors de nouveau le lemme de rapprochement. En répétant ce raisonnement k fois, k étant la distance de A et B au début de la toute première partie, on arrive à une distance nulle.

retour au texte

4. Aucun texte ne nous est parvenu à ce sujet, mais l'exposé des élèves de l'atelier au congrès 2000 précisait que, sur la surface d'un cube, un seul attaquant ne suffisait pas pour prendre la balle au défenseur.

retour au texte

Comptes Rendus MATh.en.JEANS 00-10

© MATh.en.JEANS 2002. Tous droits réservés.