Comptes Rendus MATh.en.JEANS 01-08

Enseignants : Véronique CHAUVEAU (Paris), Michel LAMARRE, Marie-Josèphe SCHMITT (Cluses).

Chercheur : Caroline JAPHET-MOUNIER (Institut Galilée, Villetaneuse)

Jumelage MATh.en.JEANS entre les lycées Charles Poncet de Cluses (74) et Camille Sée de Paris (34), année scolaire 2000-2001 (Ateliers Scientifiques).

Enoncé du problème

On dispose de nperles, chaque perle étant grise ou violette. Combien de colliers fermés circulaires différents peut-on constituer avec ces perles ? Les colliers ne différant que par une rotation sont considérés comme identiques. [...]

[...] Illustration de l¹énoncé : deux colliers  seront considérés comme identiques s¹il ne diffèrent que par rotation.

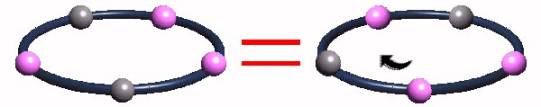
Ainsi ces deux colliers n¹en font qu¹un car il suffit de faire tourner l¹un pour obtenir l¹autre.

Par ailleurs, deux colliers symétriques seront considérés comme différents.

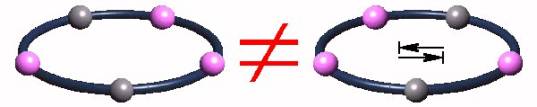
Une fois posés ces conditions, quel est alors le nombre de colliers distincts réalisables, pour un nombre fixé n de perles ?

Si l¹on prend l¹exemple d¹un collier de n = 3 perles, il nous est possible de réaliser 4 colliers différents :

Première approche de résolution

Soit S_n le nombre de colliers réalisable pour un colliers de n perles.

Il n¹est point commode de raisonner sur un collier circulaire, ainsi nous allons ouvrir le collier, le représenter par une ligne où s¹enchaînent les différentes perles le constituant, et tenter de mettre en évidence les propriétés du collier pour procéder au dénombrement.

Quand on représente un collier de n perles en ligne, on constate que pour chaque perle on à le choix entre une perle violette ou grise.

Il en est ainsi pour les n perles, chacune d¹elles nous offre 2 possibilités

Image collier 2ⁿ

On en déduit donc que le nombre de colliers en ligne possible est 2ⁿ.

Ce nombre correspond-il au différents colliers ronds réalisables ?

Si on considère ce collier et si on l¹ouvre en 2 endroits différents, à savoir à la perle 1 puis à la perle 3, on obtient les 2 représentations du collier en ligne suivantes :

Ce contre-exemple met en évidence une redondance de colliers en ligne : plusieurs colliers en ligne peuvent correspondre au même collier rond. Le nombre S_n de colliers ronds n¹est donc pas égal à 2ⁿ.

Cette redondance est une entrave au calcul de S_n,

Peut-on étudier les mécanismes de redondance ?

Quand on dispose de n = 4 perles, on peut réaliser 6 colliers et de nouveau, il se trouve qu¹un collier rond a plusieurs représentations en ligne.

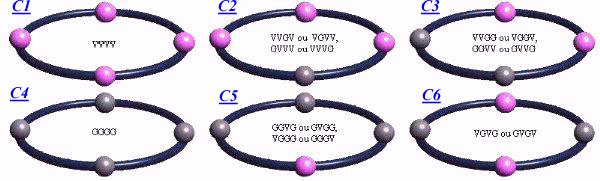
Les 3 colliers C2, C3 et C5 peuvent être désignés de 4 façons différentes alors que C6, ne peut l¹être que de  2 manières.

La redondance de colliers en lignes semble, sur cette exemple, être irrégulière, et expérimentalement pour des valeurs quelconques de n , on constate que ces répétitions sont totalement anarchiques.

Le redondance anarchique de colliers en ligne représente un obstacle sérieux à la résolution de notre problème. Nous utiliserons donc une méthode indirecte pour déterminer le nombre S_n. Nous construirons notre démonstration sur l¹analyse des propriétés que possèdent les colliers.

Une méthode de résolution indirecte :

Reprenons l¹exemple du cas où n= 3 perles.

Considérons tous les colliers qu¹il nous est possible de réaliser et écrivons sur une 1^ère colonne.

Puis pour chaque collier, on décale la perle de départ et écrit le nom décalé ainsi obtenu.

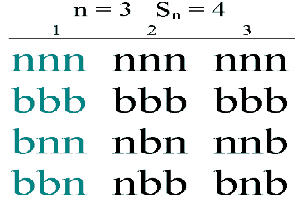
On génère ainsi, dans le cas général, une table dont la 1^ère colonne contient les colliers solutions et dont les n-1 autres les différents appellations correspondantes après un décalage, noté k, de perles.

La table est, de part sa définition, constituée de S_n lignes et de n colonnes

Appelons T le nombre total de colliers écrits à l¹intérieur : T = nx S_n

Après avoir construit la table pour quelques valeurs expérimentales de n, un examen attentif révèle que certains colliers peuvent se répéter après un certain décalage de perles.

Par exemple pour n= 6 perles, tous les colliers marqués d¹une couleur restent identiques après un certain décalage de perle.

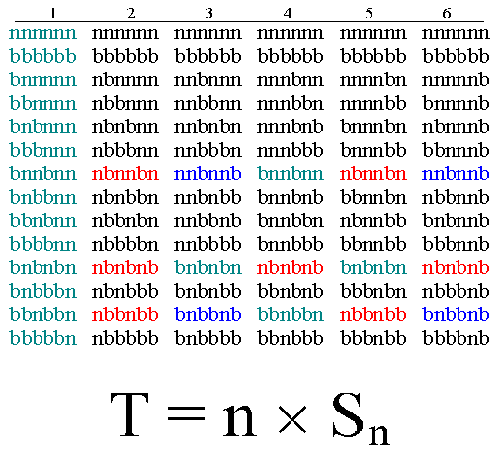
Ainsi on parvient à montrer que notre table contient :

tous les colliers qui restent identiques après un décalage de 1 perle, notés I₁,

tous les colliers qui restent identiques après un décalage de 2 perles, notés I₂,

. . .

tous les colliers qui restent identiques après un décalage de n perles, notés I_n.

Donc le nombre total de colliers écrits dans la table est :

T = nx S_n = I₁ + I₂ + ... + I_p + ... + I_n

Si l¹on parvient alors à calculer les nombres I_p, T nous sera connu et notre solution S_n se calculera par division de T par n.

Au lieu de déterminer S_n directement, cherchons l¹expression de I_p en étudiant les propriétés des colliers invariants après une décalage de k perles.

Etude de l¹invariance des colliers

Concrètement, qu¹est-ce que l¹invariance ?

Posons n = 6

Si on part de la 1^ère perle, on obtient l¹enchaînement de perles 1, 2, 3, 4, 5, 6.

Si on part de la 3^ème perle, on obtient l¹enchaînement de perles 3, 4, 5, 6, 1, 2.

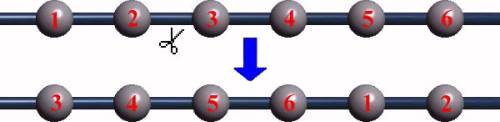
Ces deux colliers semblent identiques après décalage, donc leurs perles sont enchaînées de la même manière.

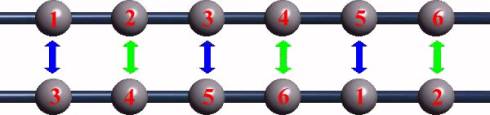
On en déduit sur cet exemple que les perles 1, 3 et 5 du colliers ont nécessairement même couleur, et de même pour les perles 2, 4, et 6. Sont définies deux relations élémentaires affectant à deux triplets de perles une même couleur.

Nous utilisons le terme « relation élémentaire », car il se trouve que grâce à ces égalités de perles, notre collier de 6 perles peut être défini entièrement à partir d¹un nombre minimal de 2 perles, les autres se déduisant de la correspondance de couleur entre perles.

Examinons une de ces relations et visualisons-la sur le collier rond.

Pour traduire le fait que 2 perles sont de même couleur, on décide de tracer un segment joignant l'une et l'autre.

Donc 1, 3 et 5 de même couleur se représente par un trait qui va de 1 à 3, un autre de 3 à 5 et un dernier de 5 à 1.

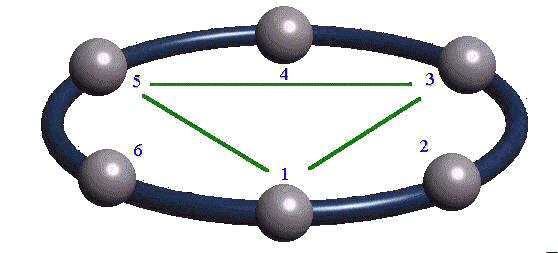
On remarque que chacun de ces segments joignant les perles 2 à 2, ce n'est pas un hasard car k = 2. Autant dire que les segments joignent les perles de ken k.

Ainsi notre méthode consiste, à partir d'une perle, à tracer des segments de k en k perles jusqu'à revenir à la perle de départ.

Quelest dans le cas général le nombre de perles liées entre elles, perles de même couleur ?

Dans le cas général, si on prend un nombre m à la fois multiple de net de k, et si on le prend le plus petit possible, il se trouve que ce m peut s'interpréter de 2 façons différentes :

- mmultiple de n: m= ax n.Balayer m perles revient à balayer  ax n perles, on peut considérer donc qu'on tourne a fois sur le cercle.

- m multiple de k: m= bx k on balaye kperles, puis kautres perles et ainsi de suite, bfois. C'est comme si on sautait de ken kperles bfois.

On peut matérialiser nos sauts par des segments entre la perle de départ et celle d'arrivée.

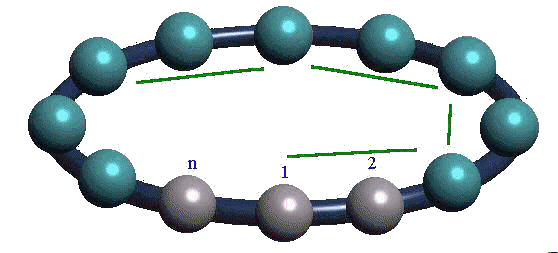
Ainsi le nombre mtraduit le fait qu'on trace bsegments en faisant atours, avec anombre minimal de tours puisque mest le plus petit multiple possible.

Au moyen de ce raisonnement, il va nous être aisé de calculer le nombre de perles qui ont même couleur dans une relation élémentaire, appelons P_k ce nombre.

On a vu que m était multiple de ket de n, et que mest le plus petit possible, on écrira donc m= PPCM ( k, n).

(Tout à l'heure, avec le nombre mque nous nous étions fixé, métait le plus petit commun multiple de ket de n, on aurait très bien pu écrire m = PPCM (k, n).)

De plus m= bx k et best le nombre de segments tracés ; donc pour obtenir b, il nous suffit de prendre met de le diviser par k donc le nombre de segments tracés, qui est aussi le nombre de perles liées entre elles (nombre que nous avons appelé P_k se calcule donc grâce à cette formule :

Ainsi, pour chaque perle, on a P_k perles qui sont de même couleur, déterminons alors le nombre de relations élémentaires, nous appelons e_k ce nombre ("e" comme "élémentaire").

Puisqu'un collier comprend nperles, que chaque perle est mise en jeu dans une relation élémentaire et qu'il y a P_k relations élémentaires, il s'en déduit aisément e_k, nombre de perles intervenant dans chaque relation élémentaire :

En remplaçant dans cette formule le nombre P_k par ce qu'il vaut, nous obtenons l'expression suivante de e_k.

Il se trouve que, considérant l'expression de e_k, une simplification peut être opérée.

Quand on multiplie 2 nombres quelconques, on obtient ainsi un produit ; et si l'on divise ce produit par le plus petit commun multiple des 2 nombres, on obtient :ce qu'en arithmétique, on appelle le PGCD, à savoir le plus grand commun diviseurs des nombre ket n.

Donc

Ainsi, pour un collier invariant après un décalage de k perles, sont définies e_k relations élémentaires qui lient des perles du collier entre elles. Pour déterminer entièrement un collier, il nous suffit de fixer e_k perles, les autres se déduisant des relations élémentaires.

Dénombrons alors les colliers qui ont la propriété d'être invariants après un décalage de kperles, nous appellerons I_k le nombre de ces colliers ("I" comme invariant, indice kpour ne pas oublier le fait que tout dépend de k).

Puisque sur les nperles, seulement e_k déterminent les colliers invariants en k, le nombre I_k est nécessairement égal au nombre de manières de créer un enchaînement de e_k perles, chaque perle pouvant prendre 2 couleurs.

Partant de ce raisonnement, on établit que :

En remplaçant ek par sa valeur, on obtient :

Lorsqu'on réfléchit sur notre table, on remarque qu'il y a des colliers qui restaient invariants après un décalage de kperles :

Certains après un décalage de 1 perle, d'autres après un décalage de 2 perles, ... jusqu'à un décalage de nperles.

Ainsi notre tableau contient tous les colliers invariants pour k= 1, il  y en a I₁, plus ceux qui sont invariants pour k = 2, [soit] I₂, et ainsi de suite jusqu'aux colliers invariants pour k= n.
T (nombre de colliers total inscrits dans la table) est égal à I₁ + I₂ + ... + I_n.

Mais souvenons nous que T = nx S_n.

Nous sommes en mesure de calculer T au moyen de I_k, S_n nous est connu,

nx

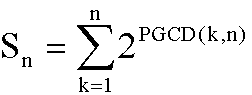
Car I_k = 2^{PGCD ( k, n)}.

Si n est [un nombre] premier, on vérifie facilement que le nombre S_n se simplifie et donne l'expression suivante.

Extension aux des colliers dont les perles prennent un nombre quelconque de couleurs

Dans notre problème nous avons raisonné seulement sur 2 couleurs mais notre raisonnement peut être étendu à un nombre quelconque de couleurs et sur le même modèle.

On établirait que pour un nombre fixé C de couleurs alors les expressions de S_n seraient les suivantes :

Pour tout n, entier naturel :

Lorsque nest premier :

Ainsi notre problème est résolu et nous sommes désormais en mesure de déterminer le nombre de colliers différents qu'il est possible de réaliser lorsque l'on dispose d'un nombre donné de perles, quand les perles peuvent prendre uniquement 2 couleurs, et même quand les perles peuvent prendre un nombre quelconque de couleurs

Remarques sur nos résultats

On remarque à la vue de l'expression simplifiée de S_n, pour npremier, que :

Puisque S_n représente un nombre de colliers, il est nécessairement entier, alors il en est de même pour (Cⁿ- C) / n

Ce qui signifie que  Cⁿ- C est divisible par n. L'explication de cette propriété est fournie par le petit théorème de Fermat, qui énonce la chose suivante :

Si p est un nombre premier, alors a , le nombre a^p-a est divisible par p.

Dans notre résolution, nous n¹avons pas considéré le cas où les colliers sont identiques par symétrie et rotation.

La résolution du problème dans ce cas nécessite l¹utilisation d¹outils théoriques beaucoup plus complexes, et contrairement à ce qui précède elle ne donne pas de caractérisation numérique des solutions.

Il s¹agit donc d¹une résolution, très abstraite sur le plan théorique, qui fournit des résultats qualitatifs et non quantitatifs, telles sont les raisons qui nous ont conduit à ne pas approfondir notre propos.

Les applications pratiques de ce problème

De plus, il se trouve, si l'on fait abstraction des colliers de perles, que nos résultats peuvent avoir un intérêt et des applications dans des domaines variés.

En résolvant ce problème nous avons été conduits à étudier l'invariance de colliers après un certain décalage de perles.

Plus généralement il arrive que l'on étudie l'invariance d'objets mathématiques après une transformation donnée. C'est notamment le cas en théorie des codes, et lorsqu'on analyse des transmissions d'informations par des signaux électriques, lumineux, sonores, etc.

D'où des applications multiples de nos résultats et de nos raisonnements.

Comptes Rendus MATh.en.JEANS 01-08

© MATh.en.JEANS 2002. Tous droits réservés.