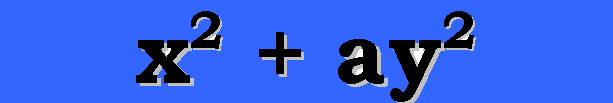
Comptes Rendus MATh.en.JEANS 01-09
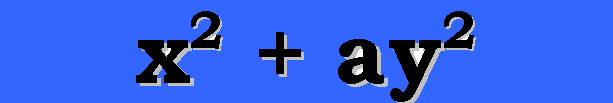
Atelier
MATh.en.JEANS du
lycée Romain Rolland d'Argenteuil (Val d'Oise). Année
scolaire 2000-2001 (atelier scientifique).
Enseignants : Dominique GUY, Fabrice LOARER
Chercheur
: Loïc ALLYS
(Université du Mans)
Sujet
Il s'agit de trouver les entiers naturels N pouvant s'écrire sous la forme :
N = x2+ ay2 avec a
{0, ±1, ± 2, ± 3} et x et y entiers relatifs.
Nous avons traité ici les deux cas : a = -1 [1ère partie] et a = +1 [2ère partie]
1a. Étude expérimentale
|
|
|
|
|
|
1 2 |
-1 impossible (*) -4 impossible (*) |
|
|
1 2 |
0 -3 impossible (*) |
|
|
1 2 |
3 0 |
|
|
|
|
|
|
1 2 ... 10 |
99 96 ... 0 |
|
|
|
(*) Remarque: "impossible" car N ne peut pas être négatif |
1b. Résultats obtenus
Nous avons fait des essais en prenant pour N toutes les valeurs entières de 0 à 170 et en essayant de les décomposer sous la forme (x-y)(x+y) [factorisation classique de l'expression x2 - y2 ]
Les premiers nombres, obtenus de cette manière pouvant s'écrire sous la forme N= x2 - y2 sont :
0,1, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17, 19, 20, 21, 23, 24, 25, 27, 28, 29, 31, ...
Par contre, nous avons observé
que ne peuvent pas s'écrire sous la forme N= x2 - y2 les nombres : 2, 6, 10, 14, 18, 22, ..
1c. Propriétés
[Théorème] (1.1) Tous les nombres impairs et les nombres pairs multiples de 4 peuvent s'écrire sous la forme x2 - y2 [et les nombres pairs non multiples de 4 ne peuvent s'écrire sous cette forme.]
Démonstration :
a) Démontrons que les nombres pairs qui sont des multiples de 4, c'est-à-dire les nombres s'écrivant sous la forme 4p, peuvent s'écrire sous la forme x2 - y2.
p est un entier naturel. 4p peut toujours s'écrire 2x2p.
Existe-t-il x et y, entiers, tels que x2 - y2 = 2x2p ?
Cette égalité est réalisée si les entiers x et y sont tels que
soit
ou
soit
Donc, quel que soit p entier naturel, on peut trouver x et
y entiers relatifs tels que 4p = x2-y2.
b) Démontrons que les nombres impairs (c'est à dire les nombres s'écrivant sous la forme 2p+1) peuvent s'écrire sous la forme x2-y2.
Existe-t-il x et y tels que x = 2p + 1 ?
Cette égalité est réalisée si :
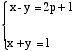 ou
ou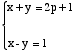
On trouve x= p+1 et y = -p , ou x= p+1 et y = p
Donc, quel que soit p entier naturel,
on peut trouver x
et y entiers relatifs
tels que 2p+1 = x2-y2
c) Démontrons que les nombres pairs qui ne sont pas multiples de 4 (c'est à dire les nombres s'écrivant sous la forme 4p+2) ne peuvent s'écrire sous la forme x2-y2
Existe-t-il x et y tels que x2-y2 = 4p+2 ?
Le nombre entier 4p+2 est forcément le produit d'un nombre pair 2m et d'un nombre impair 2m'+1, où m et m' sont des entiers naturels.
Or si x+y = 2m et x-y = 2m'+1 alors 2x = 2(m+m')+1 ce qui est impossible.
De même si x+y = 2m'+1 et x-y = 2m, alors 2x = 2(m+m')+1 ce qui est impossible.
Conclusion : Les nombres pairs qui ne
sont pas multiples de 4 ne peuvent pas s'écrire sous la
forme x2-y2. ![]()
[![]() signifie :
la preuve du théorème est
complète]
signifie :
la preuve du théorème est
complète]
2a. Étude
expérimentale
Nous avons procédé de la même manière que précédemment et nous avons obtenu les résultats suivants :
Les nombres entre 0 et 100 pouvant s'écrire sous la forme N = x2+y2 sont :
0, 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 18, 20, 25, 26, 29, 32, 34, 36, 37, 40, 41, 45, 49, 50,
52, 53, 58, 61, 64, 65, 68, 72, 73, 74, 80, 81, 82, 85, 89, 90, 97, 98, 100.
B.
Propriétés
[Théorème] (2.1) Si N est un carré parfait alors N peut s'écrire sous la forme N = x2 + y2,
Car on pourra toujours prendre
x2
= N et
y = 0 (ou
l'inverse). ![]()
Exemple :
N = 36 36 =
62+ 0 2
[Théorème] (2.2)
De plus, si
N est un carré parfait
alors N+1 =
x2+ y 2 avec x2 = N et y2
= 12![]()
[Théorème] (2.3) Si N = x2+ y 2, alors 2 N = x12 + y12
Démonstration :
On peut prendre x1 = x + y et y1 = x - y et on a bien 2N = x12 + y12
Exemple : N = 13 = 32 + 22 ; 26 = x12 + y12 [avec] x1 = 3 + 2 et y1 = 3 - 2, donc 26 = 52 + 12.
[Théorème] (2.4) S'il n'existe pas (x ; y) tel que x 2 + y2 = N, alors il n'existe pas (x1 ; y1) tel que x12 + y12 = 2N
Démonstration :
Supposons qu'il existe (x1 ; y1) tel que x12 + y12 = 2N
Peut-on trouver x et y tels que x 2 + y2 = N ?
x1 et y1 sont de même parité (c'est à dire les deux pairs ou les deux impairs), puisque la somme de leurs carrés est un nombre pair.
x12 +
y12 =
2N
![]()
![]()
![]()
![]()
![]()
[Donc,] si x1 et y1 sont de même parité, alors
x =![]() et
y=
et
y=![]() [satisfont l'égalité x 2 +
y2 = N.]
[satisfont l'égalité x 2 +
y2 = N.]
[En conclusion] si 2N est
la somme des carrés de 2 entiers, ils sont
nécessairement de même parité et N peut
s'écrire aussi comme somme des carrés de 2 entiers.![]()
[Théorème] (2.5) Si N = a2 + b2 et N' = c2 + d2, alors N N' [est de la forme] x2 + y2.
Démonstration :
On pose x = ac + bd et y = ad - bc ; [on obtient] N N' = x2 + y2 .
[Théorème] (2.6) [Dans le] cas où N est un multiple de 3, N = 3N', [le nombre] 3N' ne peut être somme de carrés d'entiers non tous deux multiples de 3. [Autrement dit si un multiple de 3 est la somme des carrés de deux entiers, ces entiers sont eux aussi multiples de 3.]
Démonstration :
[Raisonnons par l'absurde :] Supposons [que 3N = x2 + y2 et] que x et y ne soient pas multiples de 3, alors :
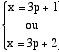 et
et
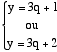 , avec p
, avec p![]()
![]() et q
et q![]()
![]() [
[![]() est l'ensemble
des entiers relatifs ]
est l'ensemble
des entiers relatifs ]
3N' = x2 + y2 équivaut à N' = ![]() ,
on a donc [suivant les 4 cas possibles] :
,
on a donc [suivant les 4 cas possibles] :
3(p2 + q2)![]()
![]() car p
car p![]()
![]() et q
et q![]()
![]()
2 ( p + q) ![]()
![]() car p
car p![]()
![]() et q
et q![]()
![]()
![]()
![]()
![]() ( ensemble des entiers naturels )
( ensemble des entiers naturels )
Conclusion: 3(p2 + q2) + 2(p+q) +![]()
![]()
![]()
[Cela contredit une des hypothèses.] Donc si x = 3p + 1 et y = 3q + 1, 3N' ne peut pas s'écrire sous la forme x2 + y2 .
[...] [Contradiction] Donc si x = 3p + 1 et y = 3q + 1, 3N' ne peut pas s'écrire sous la forme x2 + y2 .
[...] Donc si x = 3p + 1 et y = 3q + 2, 3N' ne peut pas s'écrire sous la forme x2 + y2.
[ En résumant ce qui précède, l'un des nombres x ou y doit être multiple de 3, cas qu'il convient d'examiner et qui s'avère impossible (note 1); donc x et y doivent tous deux être multiples de 3].
En résumé,
un multiple de 3 est somme des carrés de 2 entiers
[seulement] si ces entiers sont eux-mêmes multiples de
3![]()
Mais si x = 3p et y = 3q, alors, (3p)2+(3q)2 = 9(p2+q2)= 3(3p2+3q2) : ce multiple de 3 est alors aussi multiple de 9.
Conclusion
Si a =
-1, nous savons donc que seuls les
entiers naturels pairs non multiples de 4 ne peuvent s'écrire
sous la forme x2 -ay2. Mais, si
a = 1, nous n'avons obtenu que des résultats
partiels. [note
2]
Et il resterait encore à traiter les cas a = ±2 et a = ±3.
Notes des
éditeurs
Note 1. Nous complétons ici la démonstration du théorème (2.6). Quitte à échanger les rôles de x et y, on peut supposer x = 3p.
Si x = 3p et y = 3q + 1, alors
N' =![]() et on obtient N' =
3(p2 + q2) + 2q +
et on obtient N' =
3(p2 + q2) + 2q +![]()
![]()
![]()
Si x = 3p et y = 3q + 2, alors
N' =![]() et on obtient N' =
3(p2 + q2) + 4q +
et on obtient N' =
3(p2 + q2) + 4q +![]()
![]()
![]()
Dans chaque cas, 3N' ne peut pas s'écrire sous la forme x2 + y2.
Note 2. Les théorèmes (2.5) et (2.6) suggèrent en particulier d'étudier le problème lorsque N est un nombre premier, c'est à dire un nombre autre que 1 qui n'a pas d'autre diviseur que lui-même et 1.
CARRÉ SOMME DIFFERENCE EQUATION PELL ABSURDE
|
Comptes Rendus MATh.en.JEANS 01-09 |
© MATh.en.JEANS 2002. Tous droits réservés. |