L'idée est donc de se rapprocher plus du point d'abscisse b que du point d'abscisse a [parce que f(b) est plus proche de 0 que f(a)], à chaque étape, d'où le rapprochement avec le barycentre.

Dans notre démonstration, les coefficients associés correspondent aux ordonnées f(a) et f(b), [ou, plus précisément à leurs valeurs absolues].

Etape 1:

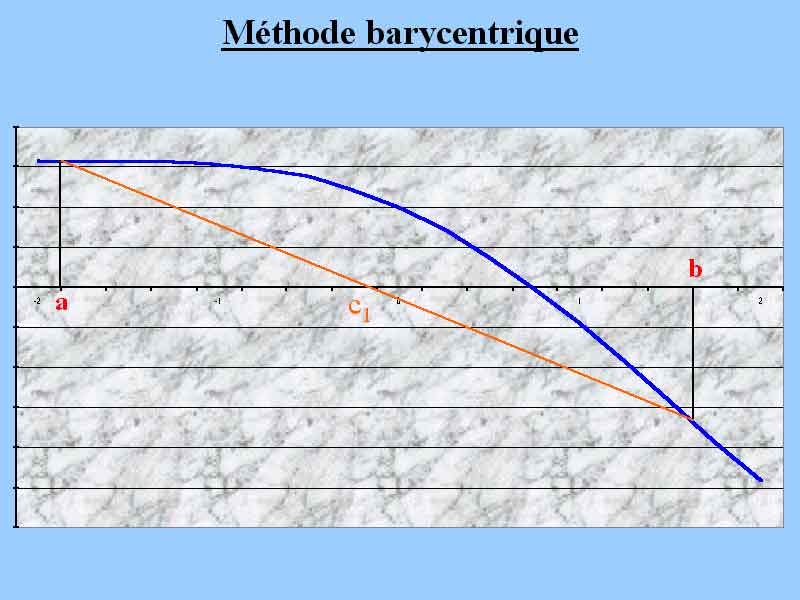
On choisi alors l'intervalle (c;b) pour continuer la procédure :

Etape 2 :

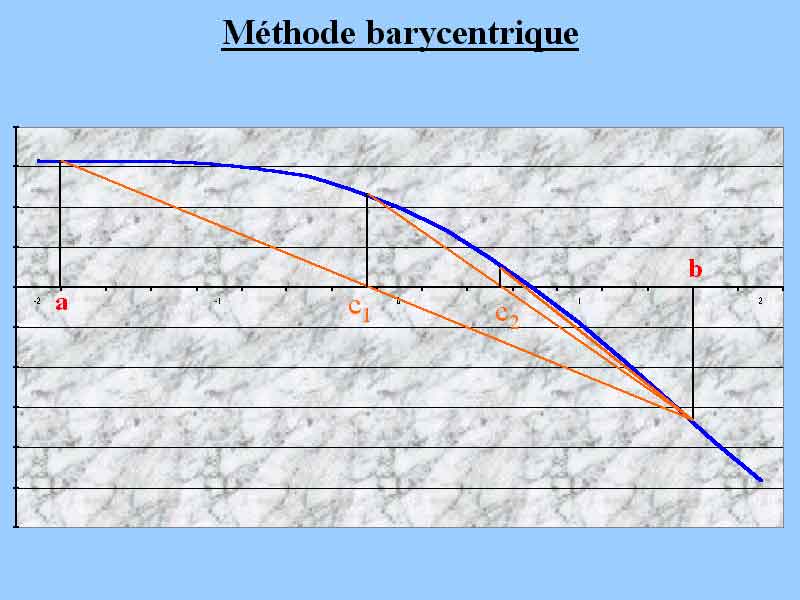
Et on itère...

On obtient c en fonction de a et b grâce à la formule suivante:

Théorème 1: Soit f une fonction continue 2 fois dérivable telle que f"(x) de signe constant, la suite (c_n) est toujours du même coté du "zéro"

Preuve du th 1

Théorème 2 :Soit f une fonction continue 2 fois dérivable telle que f"(x) de signe constant, la suite (c_n) converge vers le "zéro"

Preuve du th 2 :

On a programmé les deux méthodes sur  scilab : c'est à dire qu'on a fait calculer les c  de la suite (c_n) jusqu'à une précision définie: le nombre d'étapes est reporté sur le graphique en fonction de la précision demandée.

(On a mis en abscisse :  -log(précision) pour obtenir une courbe plus claire).

(par ici les programmes)

On constate que la méthode avec le barycentre est presque 4 fois plus rapide que la dichotomie pour une précision de 10^-15 pour l'exemple étudié avec la fonction cos(x)-x .

page suivante : Conclusion