Communiquer dans une
grille
par Bérénice BOURDIER, Janet DOMAN, Marianne
FERNANDES, Avniyé KARAKAC, Elodie LECANTE et Audrey LECLUSE.
(Classe de 3ème 2, Collège l'Ardillière de
Nézant, St Brice sous Forêt (95)).
"MATh.en.JEANS" Atelier de
recherche dans la classe ; octobre 1997- mai 1998.
enseignant : M. Bourit.
chercheurs et observateurs : Olivier Bodini, Pierre Duchet
(UPR 175 du CNRS, Paris)
Les parties de texte entre crochets [exemple] sont
de la rédaction. NDLR : note de la rédaction NDLC :
note de la copiste.
Les chiffres entre crochets renvoient aux notes ou annexes
placés en fin d'article.
____________
Texte du sujet soumis aux collégiens (Pierre Duchet, CNRS,
Paris ; © MATh.en.JEANS 1993)
"Communiquer dans une grille". Réussira-t-on à informer tout le monde
en respectant les règles de communication en vigueur dans le
réseau ?
|
Des personnes (ou des relais électroniques, si
vous préférez) sont
régulièrement disposées dans un plan.
Chaque personne peut envoyer des informations à
d'autres personnes, à condition de respecter
certaines règles.
Ces règles, bien précises et immuables,
sont les mêmes pour toutes les personnes. En fait,
à proprement parler, c'est l'ensemble de ces
règles qui définit le réseau.
|

|
Donnons un exemple de réseau, baptisé "ABC", car il est défini par trois
règles A, B et C .
|
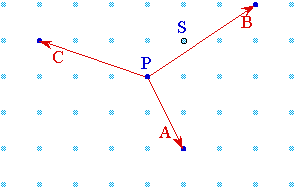
Figure 2. Exemple de réseau
|
Dans ABC, une
personne quelconque du réseau (placée en
P sur la figure 2) peut
informer
- la personne située 3 pas à l'Est, 2 pas
au Nord : c'est la règle "A".
- la personne située 3 pas à l'Ouest, 1
pas au Nord : c'est la règle "B".
- la personne située 1 pas à l'Est, 2 pas
au Sud : c'est la règle "C".
|
|
Ainsi, P ne peut pas
informer directement la personne située en
S, bien que celle-ci
soit géographiquement très proche : 1 pas vers
líEst, 1 pas vers le Nord.
Par contre, S peut
être aisément informé en trois
étapes :
- à la première étape, P prévient Q, en utilisant la
règle A.
- à la deuxième étape, Q prévient R,
en utilisant la règle B.
- à la troisième étape,
R prévient
S, en utilisant la
règle C.
|
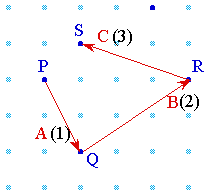
Figure 3. Information de S en 3
étapes
|
Les règles de transmission d'un réseau étant
fixées, le problème est le suivant : une nouvelle,
connue d'une personne particulière peut-elle être
transmise à tout le monde en suivant les règles du
réseau ? Sinon, quelles sont les personnes qui peuvent
être informées ?
Le problème général, qui est non
résolu à ce jour
[3], peut être
abordé sous bien des aspects :
- Si chacun diffuse immédiatement ce qu'il sait en
utilisant toutes les règles, comment se propagent les
nouvelles ? En particulier, on peut se demander combien de
personnes seront au courant au bout de 1,2, 3,..., n
étapes.
- Comment savoir si une personne choisie à l'avance
pourra être informée ? En combien d'étapes ?
De quelle manière ?
- Si on ne trouve aucun moyen de prévenir quelqu'un,
comment être vraiment sûr qu'il n'existe aucun moyen ?
- Y a-t-il des réseaux plus efficaces que d'autres pour
la diffusion ? Pour des dispositions moins
régulières des personnes à prévenir,
peut-on trouver des méthodes de diffusion rapides
générales ?
Motivation &emdash; La diffusion rapide d'une information
dans une ville, un pays, un réseau téléphonique,
peut être organisée de bien des façons : le
principe dit "du téléphone arabe" où chacun
transmet la nouvelle à ses voisins est bien connu. C'est
suivant le même principe que se propage le feu dans une
forêt (à la différence essentielle près
qu'un arbre brûlé ne transmet plus). La recherche des
meilleures organisations possibles des transmissions dans un
réseau relève de la théorie des graphes. Le
problème particulier où l'on cherche à informer
tout le monde en un minimum de temps est connu sous le nom de
"problème des ragots".
L'étude systématique des propagations
aléatoires, du type feu de forêt, utilise des techniques
mathématiques variées : les probabilités, la
théorie de la percolation (appelée ainsi à cause
de la propagation de la vapeur dans la poudre de café) et la
théorie ergodique qui étudie notamment les zones d'un
billard atteintes par une boule qui y circule indéfiniment.
(Pour d'autres aspects de la problématique des
réseaux, voir [3].)
____________
Le but de notre recherche était de savoir si on pouvait
informer tous les points d'une grille en suivant certaines
règles. Nous nous sommes intéressé à deux
cas particuliers, chacun utilisant 3 règles. [Nous avons
essayé de comprendre dans chaque cas comment augmentait le
nombre de points informés au fur et à mesure de la
transmission d'information. Les cas étudiés nous ont
conduites à des résultats différents.]
Pour notre étude, nous avons pris un repère
orthonormé (O,x,y), en nommant O le point d'origine (que le
chercheur avait noté P). [Les points qui nous intéresse
sont les points du quadrillage, c'est à dire ceux dont les
coordonnées sont des nombres entiers. Au début, seul le
point O est informé : à la première
étape, il transmet l'information à 3 points de la
grille, suivant les règles choisies. Le principe est que
chaque point qui est informé pour la première fois
à la n-ième étape transmet l'information lors de
l'étape suivante à chacun des points qu'elle peut
joindre en respectant les règles du réseau.]
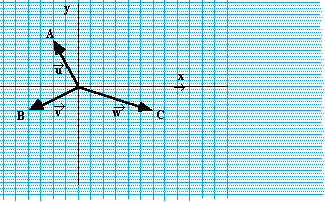
Le réseau des règles (1;-2),
(3;2) et (-3;1)
C'est celui de la Figure
2.
Première étape
A partir du point O, à la première étape, 3
points sont informés , A, B et C dont les coordonnées
sont, respectivement (1;-2), (3;2) et (-3;1).
Nous avons noté les trois règles utilisées
sous la forme suivante (Figure 4) :
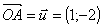 (c'est
à dire 1 vers la droite et 2 vers le bas)
(c'est
à dire 1 vers la droite et 2 vers le bas)
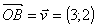 (c'est
à dire 3 vers la droite et 2 vers le haut)
(c'est
à dire 3 vers la droite et 2 vers le haut)
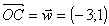 (c'est
à dire 3 vers la gauche et 1 vers le haut)
(c'est
à dire 3 vers la gauche et 1 vers le haut)
[NDLR. Ces notations sont les notations conventionnelles pour des
vecteurs du plan ; ce mot
(voir [1]) sera souvent utilisé par la
suite.]
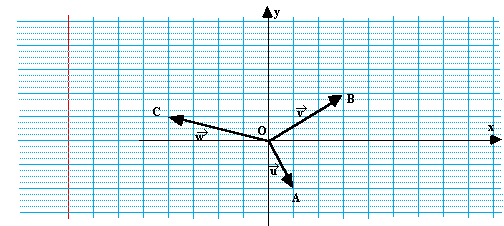 Figure 4. Les trois vecteurs de base du
réseau (étape 1)
Figure 4. Les trois vecteurs de base du
réseau (étape 1)
Deuxième étape
Les 3 points A,B,C informent, chacun, 3 nouveaux points (Figure 5)
Le point A informe D,E,F de telle façon que  ;
;  ;
; 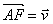 .
.
Le point B informe F,G,H de telle façon que 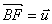 ;
; 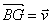 ;
; 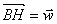 .
.
Le point C informe H,I,D de telle façon que 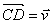 ;
; 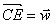 ;
; 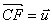 .
.
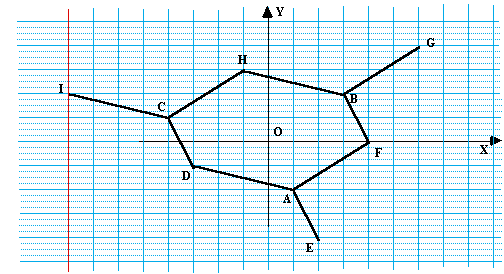
Figure 5. Etape 2
On voit que 6 nouveaux points sont informés, soit 10 points
en tout. On remarque aussi que les points D,F,H semblent être
informés deux fois, [cela "se voit" sur la figure, mais ce
n'est pas une "preuve" !]: nous allons le démontrer.
Point double
Le point D, est engendré [= informé] deux fois, par
le point A et par le point C. Nous allons essayer de le
démontrer.
Supposons que nous ayons deux points différents D et D'
(Figure 6) : par construction [et par définition], on a : 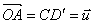 et
et 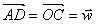 .
.
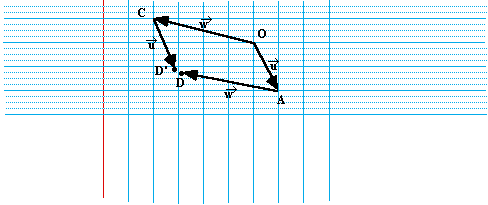
Figure 6 . Un point double.
Donc 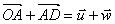 et
et 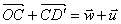 .
.
Comme l'addition [de vecteurs] est commutative, on a : 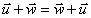 .
.
Mais [par la relation de Chasles, voir [1(a)]] 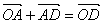 et
et 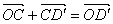 .
.
Donc 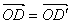 et D et D' sont le même point, mais informés par des
chemins différents. Nous dirons que D est un point
double à l'étape 2 (comme les points F et H).
et D et D' sont le même point, mais informés par des
chemins différents. Nous dirons que D est un point
double à l'étape 2 (comme les points F et H).
[Lorsqu'on connaît le principe de
l'addition vectorielle (voir
[1]), cette preuve donne une curieuse impression de
circularité : voir notre commentaire [2]
en fin d'article.]
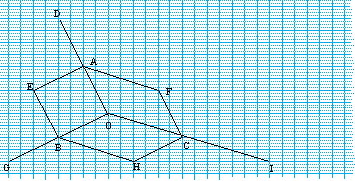
Etape n°3
Les 6 points D,E,F,G,H et I informent à leur tour, 3 points
chacun, en suivant les mêmes règles que
précédemment (Figure 7).
: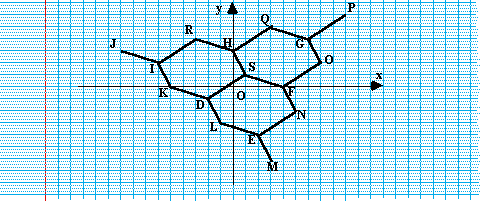 Figure 7. Etape 3
Figure 7. Etape 3
A cette étape, on remarque qu'il y a
- 3 points "simples" (informés une seule fois) :
J, M et P
- 6 points doubles (informés deux fois) :
K,L,N,O,Q et R.
- 1 point triple (informé trois fois) : S.
Etape n° 4
Les 10 points précédents J,K,L,M,N,O,P,Q,R,S
informent à leur tour 3 points chacun (Figure 8).
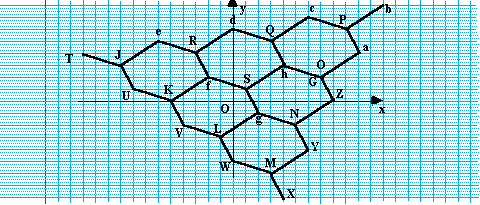 Figure 8. Etape 4
Figure 8. Etape 4
On voit qu'il y a 3 points simples, 9 points doubles et 3 points
triples.
Une loi de croissance ?
La superposition des 4 premières étapes nous montre
(Figure 9) l'ensemble des points informés.
 Figure 8. Superposition des 4 premières
étapes.
Figure 8. Superposition des 4 premières
étapes.
A partir de là le dessin devient trop compliqué pour
que l'on continue de la même manière. Heureusement, nous
avons vu une règle de croissance sur les 4 premières
étapes.
En supposant que la croissance continue toujours comme au
début (c'est notre conjecture), nous obtenons le tableau
de la Figure 9.
|
Etape n°
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Situation n°
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
G(n)
|
1
|
3
|
6
|
10
|
15
|
21
|
28
|
36
|
45
|
|
F(n)
|
1
|
4
|
10
|
20
|
35
|
56
|
84
|
120
|
165
|
Figure 9. Croissance dans le réseau
(1;-2), (3;2), (-3;1).
La troisième ligne du tableau représente le nombre
g(n) de points nouvellement informés dans la situation n
(c'est à dire après l'étape n-1). La
dernière ligne du tableau indique le nombre total T(n) de
points informés dans la situation n : on a
F(n) = g(1)+g(2)+...+g(n) ].
Nous avons trouvé une formule [qui permettrait de calculer
de proche en proche] le nombre de points nouvellement
informés.
Conjecture 1. Pour le réseau
(1;-2), (3;2), (-3;1), on a g(1)=1 et g(n+1)=g(n)+(n+1)
Exemple. g(5)+6=g(6) : 15+6=21
[ Les nombres obtenus par cette formule sont connus sous
l'appellation de nombres triangulaires : comparer avec la
Figure 2 et la formule 1 de l'article Nombres carrés
aztèques et penchés, Comptes Rendus
MATh.en.JEANS, 1998, à paraître].
Mais nous nous somme rendu compte que le problème
général n'était pas si simple : un autre groupe
s'est intéressé à d'autres vecteurs de
communication (voir ci-dessous) et dans ce cas, la croissance [du
nombre] des points informés n'est pas la même.
Le réseau des règles (-2;4)
(-4;-2), (6;-2)
Les résultats pour les trois premières étapes
(Figures 10, 11 et 12) sont [presque] les mêmes que dans le cas
précédent . Mais à la troisième
étape, on voit que le premier point triple est en fait le
point O, origine du repère. Ce qui fait qu'on obtient plus que
9 nouveaux points informés et 19 points au total , alors que
le premier tableau donnait 10 nouveaux points et 20 au total. [ La
figure 12 est analogue à la figure 7, mais les appellations
des points suivent une règle différente.]
 Figures 10 et 11. Le réseau (-2;4),
(-4;-2), (6;-2): les deux premières étapes.
Figures 10 et 11. Le réseau (-2;4),
(-4;-2), (6;-2): les deux premières étapes.
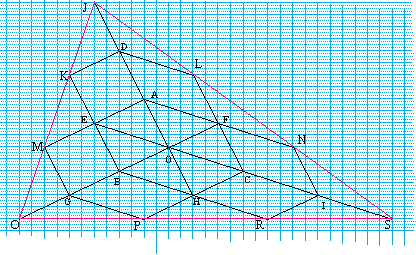 Figure 12. Le réseau (-2;4), (-4;-2),
(6;-2), la troisième étape.
Figure 12. Le réseau (-2;4), (-4;-2),
(6;-2), la troisième étape.
De plus, à partir de cette troisième étape,
le nombre de nouveaux points informés suit une croissance
régulière : il y a 3 points nouvellement
informés de plus à chaque étape , ce qui veut
dire que la fonction est une fonction affine : g(n)=3(n-1)=3n-3.
Voici les résultats que nous avons vérifiés
(tableau de la figure 13).
|
étape n°
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
situation n°
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
g(n)
|
1
|
3
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
|
F(n)
|
1
|
4
|
10
|
19
|
31
|
46
|
64
|
85
|
109
|
Figure 13. Croissance dans le réseau
(-2;4), (-4;-2), (6;-2).
Nous pensons que la loi observée se poursuit :
Conjecture 2 . Pour le réseau (-2;4), (-4;-2),
(6;-2), on a g(1)=1 et g(n) = 3(n-1) pour n>2.
Nous avons trouvé une autre raison qui
explique que nous revenons au point d'origine à la
troisième étape. En effet quand on additionne les trois
vecteurs de communication on a :
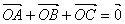
Car 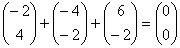 .
.
Conclusion
Nous avons trouvé deux sortes de croissance
différentes : une qui suit une loi triangulaire (comme nous
l'a dit le professeur) et une autre qui commence pareillement mais
qui ensuite devient une fonction affine (comme nous l'avons
étudié cette année).
[Outre la question de trouver une preuve pour
les conjectures 1 et 2], de nombreuse questions restent sans
réponse.[voir aussi [3]).
Question 1. Est-ce que ces lois de croissance sont les
seules qui existent ?
Question 2. Est-ce qu'il y a d'autres vecteurs qui donnent
les mêmes croissances ? Lesquels ?
Question 3. Est-ce qu'on peut informer tous les points
de la grille ?
la suite... pour d'autres élèves qui aurait envie de
reprendre cette recherche!
[Pour d'autres résultats sur le réseau (1;-2),
(3;2), (-3;1) (en particulier sur la conjecture 1 et la question 3), voir
Communication dans une grille, Actes Math.en.Jeans 1994, pp. 45- 50. Voir aussi le
commentaire [3]]
______________
Commentaires de la
rédaction
[1] Les
vecteurs
Le mot "vecteur " vient du latin vehere "porter". La
notion mathématique de vecteur du plan traduit l'idée
de translation, c'est à dire de déplacement
global des points du plan par "glissement" : une translation est une
transformation géométrique qui déplace tous les
points dans une même direction, dans un même sens et
d'une même longueur. Un vecteur peut être
mathématiquement défini de plusieurs manières
équivalentes. Voici les deux principales.
(a) Point de vue des translations. La notation 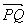 , qui se lit
"vecteur PQ", désigne l'unique translation qui transforme le
point P en le point Q. On démontre facilement que
l'écriture
, qui se lit
"vecteur PQ", désigne l'unique translation qui transforme le
point P en le point Q. On démontre facilement que
l'écriture 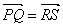 signifie que le quadrilatère PQSR (attention
à l'ordre !) est un parallélogramme.
signifie que le quadrilatère PQSR (attention
à l'ordre !) est un parallélogramme.
La composition des deux translations est encore une translation :
la translation de vecteur  suivie de la translation de vecteur
suivie de la translation de vecteur 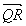 est la
translation qui transforme P en R, c'est donc la translation de
vecteur
est la
translation qui transforme P en R, c'est donc la translation de
vecteur 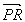 .
On dit que le vecteur
.
On dit que le vecteur 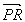 est la somme du vecteur
est la somme du vecteur 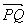 et du vecteur
et du vecteur
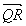 , et on
note
, et on
note 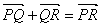 (relation de Chasles).
(relation de Chasles).
(b) Point de vue des composantes. Un vecteur 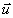 peut
être considéré comme un couple (a,b) de deux
nombres réels a et b (ces nombres sont appelés les
composantes , ou les coordonnées, du
vecteur
peut
être considéré comme un couple (a,b) de deux
nombres réels a et b (ces nombres sont appelés les
composantes , ou les coordonnées, du
vecteur 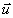 . L'addition de deux vecteurs consiste tout
simplement, par définition, à faire l'addition
composante par composante : si
. L'addition de deux vecteurs consiste tout
simplement, par définition, à faire l'addition
composante par composante : si 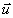 = (a,b) et
= (a,b) et 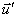 = (a';b'), on a
= (a';b'), on a 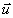 +
+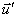 = (a+a',b+b').
= (a+a',b+b').
Pour les vecteurs, on utilise souvent une notation en
colonne : le vecteur (a,b) est noté 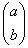 .
.
La correspondance entre les points de vue (a) et (b)
est possible dès que l'on choisit un repère du plan :
une origine O, deux axes Ox et Oy, avec une unité de mesure
sur chaque axe. Chaque point est alors repéré par le
couple de ses coordonnées dans le repère choisi. A
chaque vecteur 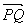 correspond un unique point M tel que
correspond un unique point M tel que 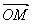 =
=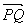 . Ce sont les
coordonnées de ce point M qui sont choisies pour
composantes du vecteur
. Ce sont les
coordonnées de ce point M qui sont choisies pour
composantes du vecteur 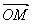 . On peut démontrer (c'est ce qui
est tenté dans l'article) que les deux définitions de
l'addition se correspondent bien : l'addition des
"vecteurs-translations" correspond à l'addition des leurs
composantes.
. On peut démontrer (c'est ce qui
est tenté dans l'article) que les deux définitions de
l'addition se correspondent bien : l'addition des
"vecteurs-translations" correspond à l'addition des leurs
composantes.
Dans les réseaux de communications qui sont
étudiés ici, la propagation de l'information au moyen
de règles de base s'écrit commodément avec
l'addition des vecteurs : par exemple si les vecteurs 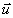 ,
, 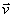 ,
, 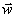 représentent les règles de base, le
fait qu'un point g soit informé à la quatrième
étape en utilisant successivement la règle
représentent les règles de base, le
fait qu'un point g soit informé à la quatrième
étape en utilisant successivement la règle 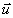 , puis la
règle
, puis la
règle 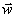 , puis la règle
, puis la règle 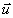 et enfin la règle
et enfin la règle 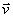 ,
s'écrit :
,
s'écrit : 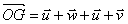 .
.
Les définitions données des vecteurs du plan et de
leur addition se généralisent sans difficulté
à l'espace (trois dimensions... ou plus!).
retour au premier
appel de la
note
[2] Remarque sur la preuve
du "point double".
La preuve que les point D et D' sont confondus utilise la
commutativité de l'addition des vecteurs. Mais comment
prouve-t-on la commutativité de l'addition
vectorielle (dont le principe est expliqué en note [1]) ?
Traditionnellement introduite en classe de 3ème,
l'égalité entre 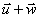 et
et 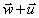 (on reprend ici les notations de la
Figure 6) est établie à partir du fait que le
point D, image de A par la translation de vecteur
(on reprend ici les notations de la
Figure 6) est établie à partir du fait que le
point D, image de A par la translation de vecteur 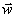 (le point A
étant lui-même défini comme l'image de O par la
translation de vecteur
(le point A
étant lui-même défini comme l'image de O par la
translation de vecteur 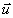 coïncide avec le point D', image de C par la
translation de vecteur
coïncide avec le point D', image de C par la
translation de vecteur 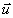 (le point C étant défini comme l'image
de O par la translation de vecteur
(le point C étant défini comme l'image
de O par la translation de vecteur 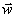 ).
).
D'où l'impression de "circularité" qui se
dégage de la preuve proposée par les collégiens.
Nous laissons au lecteur le soin d'approfondir cet exemple qui
illustre un trait essentiel de la démarche mathématique
: la distinction entre la réalité sensible (propagation
d'une information dans une grille suivant certains chemins) et le
modèle mathématique de cette réalité
(translations et addition vectorielle). Le vrai, au sens
mathématique, résulte logiquement des conventions en
vigueur dans la communauté mathématique. Le vrai, au
sens de fidélité à la réalité
sensible, résulte de la confrontation entre les conventions
des mathématiciens et notre expérience du monde
sensible.
retour au premier
appel de la note
[3] Commentaire des
chercheurs.
Le sujet proposé met en scène plusieurs domaines
actifs des mathématiques contemporaines. Les questions
posées à la fin de leur article par les
élèves relèvent de l'étude des
réseaux entiers (les "sous-groupe discrets" de lRn)
et de la "géométrie des nombres" (nombre de points d'un
réseau entiers dans une forme donnée). La recherche de
graphes particuliers permettant la diffusion rapide d'une information
relève de la Combinatoire et de la Recherche
opérationnelle. L'arithmétique est également
concernée: en se restreignant à des vecteurs de base
colinéaires du type (n;0) avec n>0, on tombe sur un
problème célèbre, proposé par
Frobénius, dont voici une version simplifiée: si
les valeurs nominales en francs des pièces en usage dans un
système monétaire sont de n1,
n2,..., nk , quels sommes sont payables
exactement dans ce système ? Le problème reste
ouvert pour k>4.
Outre les résultats présentés dans leur
article, les élèves avaient étudié une
variante inédite du problème initial : la propagation
de l'information avec la contrainte de rester dans un domaine
limité. Considérons par exemple le premier
réseau (règles (1;-2), (3;2) et (-3;1)) limité
aux points du rectangle R = [-3,+3][-2,+2] (R est le plus petit
rectangle à cotés parallèles aux axes qui
contienne les trois vecteurs de base du réseau). Nous
fûmes étonnés de constater que tous les points
à coordonnées entières de R peuvent être
informés sans sortir de R, à l'exception de l'unique
point (-3;-2) ! Nous sommes à la recherche d'une explication
générale.
Cette version limitée du problème nous parait en
tout cas très intéressante pour des recherches
ultérieures de MATh.en.JEANS.
retour au premier
appel de la note
***











