Stratégie de Huygens

Huygens(1629-1695) a commencé par tracer un demi cercle de centre O et de diamètre [AC] tel que AC = 2a, dans lequel on inscrit le triangle ACD rectangle en D et dont le côté [AD] mesure a. La corde [AE] du demi-cercle coupe la corde [CD] en F de sorte que EC = FD. Je vais vous montrer que dans ce cas AF = x = (dessin 4)

Soit OA = 1 . CEF et ADF sont deux triangles rectangles dont les angles EFC et AFD sont égaux.
Les deux triangles sont donc semblables et .
Or AD =1, donc . Mais CE =FD et CF = CD -FD

On obtient . ACD étant un triangle rectangle ,l’agent Pythagore peut venir nous aider en appliquant sa grande spécialité : son Théorème. On a CD² = AC² - AD² = 2² - 1²

 						CD   =  puis successivement      x FD = CD - FD 

xFD =-FD             FD (x +1) =            FD =           

Et là, l’agent Pythagore revient nous porter secours, le triangle FAD étant rectangle:FD² =AF² - AD² = x² - 1

On a donc :x² - 1 =

(x² - 1) (x + 1)² = 3

(x² - 1) (x² + 2x + 1) =3       

x étant nécessairement positif, x+2 l'est également.

Par conséquent la seule solution admissible est :

x = 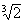      donc       AF = a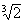   

Mais nos laboratoires ultra - secrets n’ayant pas réussi à amasser la technologie nécessaire, on ne peut obtenir la position du point E qu’à la suite de " tâtonnements ", ce qui ne me permet pas d’accomplir ma mission. Cependant, cette solution est intéressante car l’angle COE mesure PRESQUE 45°, et qu’avec une règle et un compas, il suffit de tracer la bissectrice d’un angle droit pour obtenir cette valeur.On obtient ainsi une approximation de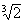

Retour