Lycée de La Mure, année 1997-1998

PROBLEME:

Premier cas:

A et B sont deux points n'appartenant pas à la droite (D).
Comment placer le point M sur (D) tel que la distance reliant ces trois points soit minimale ?

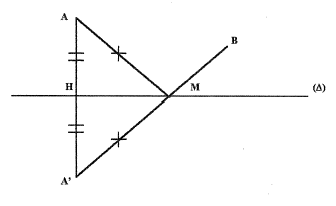
Soient deux points A et B et une droite (D) quelconque.

On trace le symétrique A' de A par rapport à (D). On trace (A'B), elle coupe alors (D) en un point M ; On a: AH = A'H et AM = A'M par propriétés sur les symétries et AM + MB=A'M + MB. Le segment [A'B] est le chemin le plus court entre les points A' et B. D'après cela on peut déduire que le point M est le point de (D) tel que la distance AM + MB soit minimale.

Deuxième cas :

Si A et B appartiennent à la droite (D), alors tout point M du segment [AB] est solution du problème posé.

PROBLEME :

Où faut-il placer le point M pour que la distance MA+MB+MC (la somme des traits pointillés) soit minimale ?

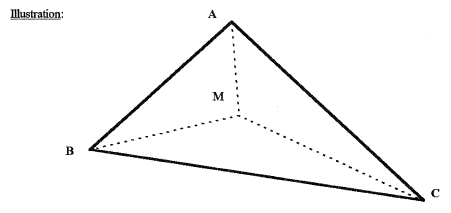
On sait que par inégalité triangulaire que

AC < AM+MC

BC < BM+MC

AB < AM+MB

donc, par addition on a : AC + AB + BC < 2AM + 2BM + 2MC d'où P/2 < MA+BM+MC, P étant le périmètre du triangle ABC.

approche expérimentale :

Pour une approche plus expérimentale du problème nous avons mis au point un programme assisté par ordinateur (compatible PC/MAC). Ce programme a pour but de nous aider à résoudre le problème du chemin minimal. Il permet de placer trois points A, B et C sur un plan, ensuite l'ordinateur affiche,un dégradé de couleur centré sur le point M tel que la somme des distances MA + MB + MC soit minimale et le point G barycentre des points pondérés (A, 1), (B, 1) et (C, 1). Cela nous a permis de constater que dans le cas où le triangle ABC est quelconque , G est différent de M.