Comptes rendus MATh.en.JEANS n° 99.03

Atelier MATh.en.JEANS des collège et lycée Romain Rolland d'Argenteuil. Atelier scientifique 1998-99.

Enseignants : Sabine GIROS et Dominique GUY

Chercheur : Loïc ALLYS (Université du Maine, Le Mans)

---

[Article vérifié et annoté : les passages entre crochets sont des éditeurs]
[ Un nombre entre crochets renvoie à une référence ]
[ L'icone renvoie au Glossaire MATh.en.JEANS , à un document ]

1) PRÉSENTATION DU JEU

Le jeu de Gründy consiste à opposer deux joueurs et qui devront partager, chacun leur tour, un tas d'allumettes en deux tas inégaux. Le gagnant est le dernier joueur à avoir joué. [note 1]

Au stand du congrès

Exemple avec 6 allumettes au départ :   

Le premier joueurpeut jouer    ceci  ou   cela   

mais en aucun cas n'a le droit de jouer   ceci .

Si a joué
	est obligé de jouer avec [le tas]
	peut jouer        ou bien       (le tas de 1 allumette n'a pas été touché).

Il y a deux parties possibles :

On note [cette partie] :

6 5 + 1 3 + 2 + 1 2 + 1 + 2 + 1.

Ainsi, dans cette partie, c'est  qui a gagné, car c'est le dernier à jouer :  ne peut recouper aucun tas.

Mais, dans la partie :

On note [cette partie] :

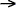
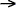
6 5 + 1 4 + 1 + 1 3 + 1 + 1 + 1 2 + 1 + 1 + 1 + 1

C'est    qui gagne.

2) SUJET DE RECHERCHE

Nous avons cherché à savoir si certaines situations permettaient au premier joueur de gagner systématiquement (ce qui serait logique car il influence le jeu en premier) et si certaines situations permettaient, au contraire, au second joueur de gagner.

Nous supposons que les deux joueurs utilisent toujours la bonne stratégie (qui est à préciser d'ailleurs) c'est-à-dire qu'aucun des deux joueurs ne jouera volontairement une situation qui l'amènerait à perdre s'il peut faire autrement. Ainsi lorsqu'un joueur perdra, c'est qu'il n'aura pas de choix possibles l'amenant à gagner.

Exemple 2.1 [la situation 7] :

7 4 + 3 4 + 2 + 1 3 + 1 + 2 + 1 2 + 1 + 1 + 2 + 1
le joueur  gagne. Ainsi le joueur  ne va pas jouer 4 + 3 au départ mais :

7 5 + 2 3 + 2 + 2 2 + 1 + 2 + 2
le joueur  gagne. Mais le joueur  peut s'y prendre autrement (ce qu'il fait, donc)

7 5 + 2 4 + 1 + 2 3 + 1 + 1 + 2 2 + 1 + 1 + 1 + 2 , ce qui lui permet de gagner.

Premières constatations :

• Un tas de 1 allumette ne peut être recoupé car il ne se partage pas
• Un tas de 2 allumettes ne peut être recoupé car il ne se partage pas en deux tas inégaux.

De ce fait, dans la suite, nous ne tiendrons plus compte de ces deux nombres dans les décompositions.

[On appelle décomposition d'une situation, toute situation qui peut lui succéder suivant les règles du jeu.]

Avec cette remarque, le dernier exemple de partie devient :

7 5 4 3 2     (plus facile à lire).

On notera aussi 5 + 2 5. (Le symbole ne correspond pas à un tour de jeu mais à une simplification.)

3) METHODE EMPLOYEE

A) Définitions

[ Nous faisons une convention préalable ]

On a décidé d'appeler situation perdante, une situation où le joueur qui commence à jouer est sûr de perdre et de même situation gagnante, une situation où celui qui commence à jouer est sûr de gagner. En fait, on se réfère au premier joueur [= au joueur qui doit jouer en premier dans cette la situation] pour savoir si une situation est gagnante ou perdante.

Exemple 3.1 : Traitons les cas [d'un tas] de 4 et [celui d'un tas] de 5

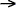
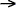
4 3 2 : le joueur est gagnant, cependant, le joueur n'a pas d'autre choix possible.

Ainsi, 4 est une situation perdante .

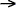
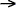
5 3 2 le joueur gagne
mais le joueur a une autre possibilité :

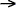
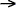
5 4 3 2 : et il gagne .

En offrant le 4 (perdant) , le joueur  est sûr de gagner. Ainsi, le 5 est gagnant.

D'après l'exemple 2.1 vous pouvez remarquer que 7 est perdant.

Nous constatons aussi, avec ces exemples, et particulièrement celui de 5, que donner une situation perdante à son adversaire est une stratégie. D'où une plus grande nécessité de connaître la liste ( une liste ) des perdants et des gagnants. Pour la construire, en décomposant tour à tour les nombres les uns après les autres, nous avons utilisé la propriété inhérente à notre définition de perdant et de gagnant suivante :

Exemples 3.3 :

• Le 4 est perdant car toutes ses décompositions ( 4 3 +1 ) sont gagnantes
• Le 5 est gagnant car la décomposition 5 4 + 1 4 est perdante
• Le 6 est gagnant car la décomposition 6 4 + 2 4 est perdante
• La situation 4 + 3 est gagnante car la décomposition 4 + 3 4 + 2 + 1 4 est perdante
• Le 7 est perdant car toutes les décompositions (7 6 + 1 6 ou bien 7 5 + 2 5 ou bien 7 4 + 3 ) sont gagnantes.

B) Suppression de certains tas

• Les perdants

Nous avons déjà vu que nous pouvions supprimer les tas de 1 ou de 2 allumettes. En fait nous pouvons supprimer toutes les situations perdantes car lorsqu'on commence à jouer une situation perdante, notre adversaire a toujours quelque chose à faire après nous ( c'est d'ailleurs pour cela que l'on perd ! ! ! ). Ou encore, une situation perdante sera réglée en un nombre pair de coups. [En d'autres termes  :]

[Théorème 3.4 ]

• [ La nature d'une situation ne change pas si on lui ajoute ou si on lui enlève une situation perdante].

Exemple 3.3 :

4 3 2 et 4 + 3 3 +1 + 3 2 + 1 + 1 + 3 3 c'est toujours au même joueur de jouer.
Ainsi 4 + 3 3 et le 4 a été supprimé.

[Pour une preuve du théorème 1 voir la note 2].

• Les doubles

Un double est une situation où il y a deux tas ayant le même nombre d'allumettes. [note 3]

Un double peut être supprimé car c'est une situation perdante. En effet, notre adversaire aura toujours le moyen de copier ce que l'on vient de faire. [note 4]

[Théorème 3.5 ]

• [Un double est une situation perdante].

Exemples 3.4 :

• 4 + 4 3 + 4 3 + 3 2 + 3 2 + 2 le joueur   n°1gagne
• 5 + 5 4 + 5 4 + 4 ou 5 + 5 3 + 5 3 + 3 le joueur  n°1 gagne.

C) Tableau des situations initiales gagnantes et perdantes

Ci-dessous un tableau, construit par nos soins jusqu'à 27 et complété jusqu'à 50 grâce à J.H Conway (On numbers and games [note 5] )

4) SITUATIONS DE MEME TYPE

[Comment savoir si une situation est gagnante ou perdante lorsqu'elle est obtenue par somme de deux autres situations ? La seule distinction "perdant" ou "gagnant" va s'avérer insuffisante pour répondre à ce problème. Nous allons introduire des "types de situation" pour mieux classer les situations.]

A) Différents cas :

En partant du couplage des situations gagnantes et perdantes, les cas possibles sont :

Perdant et perdant noté (P) + (P) , ex : 7 + 4

Perdant et gagnant noté (P) + (G) , ex : 4 + 5

Gagnant et gagnant noté (G) + (G) , ex : 5 + 3 . [note 6]

Nous avons cherché à savoir si ces cas étaient des situations gagnantes ou perdantes.

Or : (P) + (P) (P) par suppression d'un tas perdant ( voir §3B [théorème 2]). De même : (P) + (G) (G)

Par contre, deux gagnants ensemble peuvent créer une situation gagnante ou une situation perdante suivant les cas :

Exemples 4.1 :

(G) + (G) [peut être] (P) :  5 + 5 est une situation perdante puisque c'est un double

Mais (G)+(G) [peut être] (G) : 5 + 3 3 + 2 + 3 3 + 3 ainsi, 5 + 3 est une situation gagnante ( car Š, petit rappel, elle se décompose en une situation perdante ( 3 + 3 )).

B) Cas Gagnant + Gagnant

Nous avons vu qu'il y avait deux cas différents avec Gagnant + Gagnant.

[Définition 4.2 ] Nous avons décidé d'appeler :

• Gagnants de même type , deux gagnants qui donnent, ensemble, une situation perdante.
  C'est à dire (G)+(G) (P) .
• Gagnants de type différents , deux gagnants qui donnent, ensemble, une situation gagnante.
  Soit (G)+(G) (G)

Exemples 4.3 :

• d'après l'exemple 4.1, 5 et 3 sont de types différents
• Voici la liste des décompositions possibles de 6 + 3
  6 + 3 5+1 + 3 (G)
  4+2 + 3 3 (G)
  6 + 2+1 6 (G)

  elles sont toutes gagnantes. Ainsi, 6 + 3 est perdant et, 6 et 3 sont de même type. [note 7]
  .

C) Tableau des différents types

Le tableau ci-dessous s'est construit au fur et à mesure. Nous vous expliquons sa construction jusqu'au nombre 8 , nous l'avions construit jusqu'à 27 et nous vous le donnons jusqu'à 50 grâce à J.H Conway ( On numbers and games ), toujours.

• Le type T₀ est le premier rencontré, celui de 0, 1 ou 2, c'est à dire le type des Perdants.
• Le nombre 3 est gagnant, il n'est donc pas de type T₀, il sera de type T₁
• 4 étant perdant sera de type T₀
• Le nombre 5 est un gagnant de type différent que 3 (exemple 4.2), par conséquent, il se trouve dans une autre colonne : T₂
• Puis 6 est un gagnant de même type que 3 (exemple 4.2). Ainsi, il sera dans la même colonne : T₁
• Le 7 est perdant (exemple 2.1) et donc de type T₀
• Enfin, le 8 est gagnant ( car Š : 7 + 1 est une décomposition perdante ). De quel type est il ?

  - Est il du type de 3 ? Décomposons 8 + 3

  8 + 3 7 + 3 3 (G)

  8 + 3 6 + 3 (P) (car 6 et 3 sont de même type)

  On trouve une décomposition perdante, ainsi 8 + 3 est gagnant et donc 8 et 3 sont de types différents et 8 n'est pas dans la colonne T₁

  - Est il du type de 5 ? Décomposons 8 + 5

  8 + 5   7 + 5 5 (G)
  6 + 5 (G)
  5+3 + 5 3 (G)
  8 + 4 8 (G)
  8 + 3 (G)

  Toutes les décompositions étant gagnantes, 8 + 5 est une situation perdante, ainsi 8 et 5 sont de même type et 8 est de type T₂.

Finalement, [on peut résumer comme ci-dessous la définition des types pour les situations comportant un seul tas.]

[Définition 4.4 ] [On attribue de proche en proche un type aux situations 0,1,2,3 ...., avec la règle suivante :

• si la situation N est de même type (au sens de la définition 4.2) qu'une des situations précédentes, soit N' avec N'<N  ; le type de la situation N est alors celui de N'. (note 8)
• sinon, le type de la situation N est T_k , où k est le plus petit numéro manquant dans les numéros des types apparus précédement.]

[Selon cette définition,] nous avons le tableau suivant [qui donne la classification des 50 premières situations suivant leur type] :

5) TRAVAIL SUR LES TYPES

A) Mélange des types

On peut se demander comment vont réagir des configurations réalisées à partir des différents types.

[La question étudiée est la suivante : A et B étant des situations d'un type connu, peut-on attribuer un type à la situation A+B  ? (note 9)]

On voit très vite pourquoi, par exemple, T₀ + T₀ T₀. En effet, deux perdants ensemble donnent une situation perdante.
De même, rapidement, on a T₀ + T_i T_i puisque l'on peut supprimer tout perdant dans une décomposition .
D'autre part, et par définition des gagnants de même type, T_i + T_i T₀ .

Reste à étudier les mélanges un peu moins évidents de types.

• Commençons par T₁ + T₂ , on sait ( gagnants de types différents ) que c'est une situation gagnante, mais de quel type est-elle ?

  -De type T₁ ? Pour cela, il faudrait que T₁ + T₂ + T₁ T₀, or, T₁ + T₂ + T₁ T₂  puisque T₁ + T₁ T₀ , et que l'on peut le supprimer. Ainsi T₁ + T₂ n'est pas de type T₁ .

  -De type T₂ ? Comme précédemment, T₁ + T₂ + T₂  T₁  et pas T₀  et donc T₁ + T₂  n'est pas de type T₂ .

  -De type T₃ ? Regardons la décomposition d'une situation T₁ + T₂ + T₃

  Par exemple :

  3 + 5 + 13 5 + 13 (G)

  3 + 4 + 13 3 + 13 (G)
  3 + 3 + 13 13 (G)
  3 + 5 + 12 5 (G)
  3 + 5 + 11 3 + 5 (G)
  3 + 5 + 10 + 3 5 + 10 5 (G)
  3 + 5 + 9 + 4 3 + 5 + 9 5 (G)
  3 + 5 + 8 + 5 3 + 8 (G)
  3 + 5 + 7 + 6 3 + 5 + 6 5 (G)

  Ainsi, 3 + 5 + 13 est une situation perdante et 3 + 5 est du même type que 13, soit T₁ + T₂ T₃ .

  De cette règle, on déduit : T₁ + T₃ + T₂ T₃ + T₃ T₀ . Soit : T₁ + T₃ T₂

  Et de même, T₂ + T₃ T₁ .

• [Combinaisons] avec T₄ :  
  • T₁ + T₄  est gagnant mais de quel type ?

    - Il ne peut pas être de type T₁ ni T₄ ( voir pour T₁ + T₂ qui n'est ni T₁ ni T₂ ).

    -Est-il de type T₂ ?  T₁ + T₄ + T₂ T₃ + T₄ , qui n'est pas perdant, donc T₁ + T₄  n'est pas de type T₂ .

    -De même, T₁ + T₄  n'est pas de type T₃ .

    -Voyons s'il est de type T₅ [en cherchant le type de T₁ +T₄ +T₅ ] : essayons avec les décompositions de 3 + 18 + 41 .

    3 + 18 + 41 18 + 41 (G)

    3 + 18 + 40 18 (G)
    3 + 18 + 39 3 (G)
    3 + 18 + 38 + 3 18 + 38 (G)
    3 + 18 + 37 + 4 3 + 18 + 37 18 (G)
    3 + 18 + 36 + 5 3 + 5 (G)
    3 + 18 + 35 + 6 18 + 35 (G) il faut continuer :

    3 + 18 + 41 3 + 18 + 34 + 7 3 + 18 +34 18 (G)

    3 + 18 + 33 + 8 3 + 8 (G)
    3 + 18 + 32 + 9 18 + 32 (G)
    3 + 18 + 31 + 10 3 + 18 + 31 18 (G)
    3 + 18 + 30 + 11 18 (G)   ( car 3 + 30 + 11 T1 + T3 + T2 T0)
    3 + 18 + 29 + 12 18 +29 (G)
    3 + 18 + 28 + 13 18 + 13 (G)
    3 + 18 + 27 + 14 3 + 14 (G)
    3 + 18 + 26 + 15 3 + 18 + 15 18 (G)
    3 + 18 + 25 + 16 3 + 18 (G)
    3 + 18 + 24 + 17 3 + 17 (G)
    3 + 18 + 23 + 18 3 + 23 3 (G)
    3 + 18 + 22 + 19 3 + 18 (G)
    3 + 18 + 21 + 20 3 + 18 + 21 3 (G)

    Reste le 18 à décomposer.

    3 + 18 + 41 3 + 41 + 17 T₁ + T₂ + 41 T₃ + 41 (G)

    3 + 41 + 16 T₁ + T₃ + 41 T₂ + 41 (G)
    3 + 41 + 15 + 3 41 + 15 (G)
    3 + 41 + 14 + 4 3 + 41 +14 T₁ + T₂ + 41 T₃ + 41 (G)
    3 + 41 + 13 + 5 T₁ + T₂ + T₃ + 41 T₀ + 41 41 (G)
    3 + 41 + 12 + 6 41 + 12 (G)
    3 + 41 + 11 + 7 3 + 41 + 11 T₁ + T₂ + 41 T₃ + 41 (G)
    3 + 41 + 10 + 8 3 + 41 + 8 T₁ + T₂ + 41 T₃ + 41 (G)

    Enfin, toutes les décompositions sont gagnantes et donc 3 + 18 + 41 est perdant, et donc 3 + 18 et 41 sont de même type soit :
    T₁ + T₄ T₅ .

  • De cette règle on peut déduire T₁ + T₅ T₄  et T₄ + T₅ T₁
  • Ensuite pour T₂ + T₄ : il n'est ni T₁ ni T₂ ni T₃ ni T₄ ni T₅ : en effet :

    T₂ + T₄ + T₁ T₃ + T₄ (G)
    T₂ + T₄ + T₄ T₂ (G)
    T₂ + T₄ + T₂ T₄ (G)
    T₂ + T₄ + T₅ T₂ + T₁ (G)
    T₂ + T₄ + T₃ T₄ + T₁ (G)

    on va donc nommer T₆ son nouveau type [note 10]. Ainsi T2 + T4 T6

    Il s'ensuit que T₂ + T₆ T₄ [et que] T₄ + T₆ T₂

  • T₃ + T₄  est gagnant mais ni T₁ ni T₂ ni T₃ ni T₄ ni T₅ ni T₆ ( le raisonnement est le même que pour T₂ + T₄ ) . Ainsi : T₃ + T₄ T₇  [note 11] . [On en déduit] T₇ + T₄ T₃ [et ] T₇ + T₃ T₃
    
• [Combinaisons] avec T₅ .
  Certains cas ont déjà été traités. Pour ceux qui restent :
  • T₂ + T₅ T₁ + T₃ + T₅ T₃ + T₄ T₇ donc T₂ + T₅ T₇ .
  • De même : T₃ + T₅ T₂ + T₁ + T₅ T₂ + T₄ T₆ donc T₃ + T₅ T₆ .
  • Puis, des deux règles précédentes, on déduit : T₅ + T₆ T₃
  • T₅ + T₇ T₂
  • T₂ + T₇ T₅
  • T₃ + T₆ T₅
    
• [Combinaisons] avec T₆ .
  • T₁ + T₆ T₁ + T₂ + T₄ T₃ + T₄ T₇ soit T₁ + T₆ T₇
  • Et donc T₆ + T₇ T₁
  • [et] T₁ + T₇ T₆
• [Combinaisons] avec T₇ .
  Tous les cas ont déjà été traités.

[Théorème 5.1] Récapitulatif :[note 12]

T1 + T2 T3
T1 + T3 T2	T2 + T3 T1
T1 + T4 T5	T2 + T4 T6	T3 + T4 T7
T1 + T5 T4	T2 + T5 T7	T3 + T5 T6	T4 + T5 T1
T1 + T6 T7	T2 + T6 T4	T3 + T6 T5	T4 + T6 T2	T5 + T6 T3
T1 + T7 T6	T2 + T7 T5	T3 + T7 T4	T4 + T7 T3	T5 + T7 T2	T6 + T7 T1

B) Détermination du type d'une situation

Lors de la décomposition d'une situation, nous avons fait une constatation que nous n'avons pas démontré :

Exemple 5.3. Pour [la situation] 19 : cherchons le type de toutes ses décompositions

19 18 T₄

17 T₂
16 + 3 T₃ + T₁ T₂
15 + 4 15 T₁
14 + 5 T₀
13 + 6 T₃ + T₁ T₂
12 + 7 12 T₁
11 + 8 T₀
10 + 9 9 T₁

Ainsi, le plus petit type manquant est le type 3, qui est celui de 19.

Exemple 5.4. Autre exemple : pour 29 :

29 28 T₁

27 T₄
26 + 3 3 T₁
25 + 4 25 T₃
24 + 5 T₄ + T₂ T₆
23 + 6 6 T₁
22 + 7 22 T₃
21 + 8 T₄ + T₂ T₆
20 + 9 9 T₁
19 + 10 19 T₃
18 + 11 T₄ + T₂ T₆
17 + 12 T₂ + T₁ T₃
16 + 13 T₀
15 + 14 T₁ + T₂ T₃

Le plus petit type qu'il manque est T₂ et c'est en effet celui de 29.

Note 1. Gründy proposa ce jeu en 1939. En dépit du calcul des 10.000.000 premiers cas par R. Guy, ce jeu continue à défier toute analyse complète.

retour à l'appel de cette note

Note 2. Une situation de jeu est soit perdante ou gagnante, c'est ce que nous nommons la "nature" de cette situation : par définition deux situations de même nature sont équivalentes.Le théorème énoncé se formule plus précisément de la manière suivante : Si P est une situation perdante et X une situation quelconque, alors la situation P+X (situation "somme", obtenue en réunissant en un seul ensemble de tas l'ensemble de tas P et l'ensemble de tas X), est équivalente à la situation X.

Une preuve rigoureuse de ce résultat s'obtient en deux étapes, en faisant intervenir les jeux P et X qui correspondent (séparément) aux situations P et X. Le jeu qui correspond à la situation P+X est noté P+X.

1ère étape : si X est perdante, P+X est perdante.
En effet, pour chacun des jeux P et X, (le second joueur) dispose d'une stratégie gagnante ; gagne alors dans le jeu P+X avec la stratégie suivante :

lorsque joue "dans P" (c'est à dire en divisant un tas de P), répond "dans P", conformément à la stratégie gagnante du jeu P
lorsque joue "dans X" (c'est à dire en divisant un tas de X), répond "dans X", conformément à la stratégie gagnante du jeu X.

2ème étape : si X est gagnante, P+X est gagnante.
En effet, devant la situation P+X, joue "dans X" conformément à la stratégie gagnante qu'il connaît pour le jeu X. La nouvelle situation est alors de la forme P+X' où X' est perdante. D'après notre première étape, P+X' est perdante. Il en résulte que P+X est gagnante (rappelons qu'un situation est gagnante si une de ses décompositions est perdante !).

Le jeu noté P+X est couramment appelé le jeu somme des jeux P et X. C'est la nature d'un jeu somme qui est recherchée dans la suite de l'article.

retour à l'appel de cette note

Note 3. Plus généralement, on pourrait appeler double la réunion de deux situations identiques. Les résultats qui suivent s'appliquent sans changement avec cette définition.

retour à l'appel de cette note

Note 4. La stratégie qui permet à (deuxième joueur) de gagner à partir d'une situation "double" de la forme S+S est la suivante : (premier joueur) joue ce qu'il veut dans l'un des deux exemplaires de S, et répond en jouant la même chose dans l'autre exemplaire de S. La situation qui en résulte sera encore "double" : avec cette stratégie d'imitation,sera forcément le dernier à jouer. Autrement dit : le jeu somme (voir note 2) de deux jeux identiques est perdant (pour le premier joueur).

retour à l'appel de cette note

Note 5. J.H. Conway, On numbers and Games, Academic Press, New York, 1976. L'encyclopédie en ligne des suites d'entiers de Sloane () donne les valeurs suivantes pour les tas perdants : 0,1,2,4,7,10,20,23,26,50,53,270,273,276,282,285,288,316,334,337,340,346,359,362,365,386,389,392,566,630,633,636,639,673,676,682,685,923,926,929,932,1222,...

retour à l'appel de cette note

Note 6. C'est nous qui avons introduit ces notations (G) et (P) pour ne pas confondre les classes de situations avec les situations elle-mêmes. On peut lire «(G)» comme «une situation de la classe "gagnant"» et «(P)» comme «une situation de la classe "perdant"».

retour à l'appel de cette note

Note 7. Il est normal de se demander ici si l'appellation "situation de même type" est bien choisie. Deux situations A et B qui sont, chacune, de même type qu'une autre situation C sont-elles, elles-aussi de même type ? Autrement dit, sachant que A+C et B+C sont des situations perdantes, est-il vrai que A+B est elle aussi perdante ? Fort heureusement, cela est bien le cas. en effet C+C est perdante d'après le théorème des "doubles" (Théorème 3.5), donc, d'après le théorème 3.4, on a A+B A+B +C+C. Or cette dernière situation est la somme des deux situations perdantes A+C et B+C, donc est perdante d'après le théorème 3.4. Cela prouve la transitivité de la relation "A est de même type que B" . Cette relation étant également réflexive (car A+A est perdante) et symétrique (car A+B=B+A), c'est une relation d'équivalence.

retour à l'appel de cette note

Note 8. Ici, nous avons vraiment besoin d'être sûr que deux situations du même type que N sont de même type, Cela a été prouvé dans la note 7.

retour à l'appel de cette note

Note 9. Dans la suite, les auteurs utilisent sans le dire la propriété suivante : Si A et A' sont de même type, et si B et B' sont de même type , alors A+B et A'+B' sont de même type. Cela est très facile à prouver : si A+A' et B+B' sont perdantes, A+A'+B+B' est perdante d'après le théorème 3.4. autrement dit A+B et A'+B' sont de même type.

retour à l'appel de cette note

Note 10. Cette définition du type T₆ est incorrecte, car T₆ a déjà été défini par la définition 4.4 comme le type d'une situation gagnante à un seul tas qui s'avère de type différent des types précédemment apparus T₁ , T₂ , T₃ , T₄ , T₅ . On peut prouver que  T₂+ T₄ est effectivement de type T₆ , de la même manière que l'on avait prouvé précédemment que T₁+ T₄  était de type T₅ , c'est à dire en considérant les décompositions de T₂ + T₄+ T₆ et en montrant qu'elles sont toutes gagnantes,

retour à l'appel de cette note

Note 11. Même remarque que dans la note 10 : le type T₇ ayant déjà été introduit comme type d'une certaine situation à un seul tas, pour prouver que  T₃+ T₄ est de type T₇ , il faut établir que toutes les décompositions de T₃+ T₄ + T₇ sont gagnantes.

retour à l'appel de cette note

Note 12. Une conclusion simple sur le "mélange des types" apparaît ici : la somme de deux situations à un seul tas, a pour type celui d'une situation à un seul tas . cette "loi" (faute de preuve générale, il s'agit encore d'une conjecture) vient d'être établie pour les types T₀ , T₁ , jusqu'à T₇.

retour à l'appel de cette note

Note 13. Historiquement, c'est la propriété énoncée par la conjecture 5.2 qui a servi à Gründy (et, indépendamment à Sprague) pour introduire la fameuse "fonction de Sprague-Gründy", fonction qui attribue une valeur entière à chaque position d'un jeu de NIM .

retour à l'appel de cette note

nombre entier jeu de gründy tas d'allumettes jeu de nim fonction de gründy addition de nim