Comptes Rendus MATh.en.JEANS 99-10

Enseignants : Michel LAMARRE et Marie-José SCHMITT (Charles Poncet) ; Véronique CHAUVEAU (Camille Sée).

Chercheur : Jean-Christophe NOVELLI (ENS, Paris).

Jumelage MATh.en.JEANS entre les lycées Charles Poncet à Cluses (74) et Camille Sée à Paris (93). Ateliers de Pratique Scientifique, année scolaire 1998-1999.

---

[Article vérifié et annoté : les passages entre crochets sont des éditeurs]

[ L'icone renvoie au Glossaire MATh.en.JEANS , à un document ]

[Résumé. Prenons un nombre entier positif n. De combien de façons peut-on écrire n , comme somme de nombres entiers positifs ? Le sens de la question varie selon que l'on considère des sommes ordonnées ou non : une composition de n sera une suite d'entiers positifs de somme n (ainsi (1,2,2) et (2,1,2) seront deux compositions distinctes de l'entier 5) tandis qu'une partition de n sera une liste d'entiers positifs, de somme n, rangée par ordre croissant (ainsi 1+2+2 et 2+1+2 seront des écritures différentes de la même partition du nombre 5, soit (1,2,2)). Les auteurs montrent que le nombre A( n) de compositions de n vaut 2^n-1. Pour le nombre P( n) de partitions de l'entier n, ils donnent une expression simple de la série génératrice correspondante, c'est à dire de la somme infinie 1+ P(1)X¹+ P(2)X²+ P(3)X³+ ... .]

[Introduction]

Notre lycée est situé à Cluses, en Haute - Savoie (74). Nous avons fêté l'année dernière son 150 ème anniversaire (note 1). Onze élèves de différentes classes ont suivi tout au long de l'année Math.en.Jeans (note 2). Nous avons été encadrés par deux professeurs de mathématiques, Mme Schmitt et M. Lamarre, et par un chercheur, Jean - Christophe Novelli. Nous profitons d'ailleurs de cet article [qui est est un compte rendu de notre exposé au congrès] pour les remercier[...].

[Le sujet]  Soit n un entier non nul. On appelle partition de n toute suite décroissante d'entiers non nuls dont la somme vaut n. Il s'agit de trouver une manière de compter rapidement le nombre de partitions de n.

[Une partition de n est donc une décomposition de n en somme d'entiers positifs rangés dans l'ordre croissant : nous avons commencé l'étude de cette question en dénombrant d'abord les "compositions" de l'entier n, c'est à dire toutes les écritures possibles de n comme somme d'entiers positifs.]

[Soit n un entier non nul. On appelle composition de n une suite d'entiers non nuls dont la somme vaut n. Nous notons A( n) le nombre de compositions de l'entier n]

I.1

I.2

Jusqu'à 3, trouver les compositions d'un nombre est faisable, mais le nombre A(n) croît très vite, en fonction de n. [Afficher] le tableau de valeurs de A(n) et P(n)

Nous cherchons à trouver une méthode nous permettant de trouver les compositions d'un nombre à partir des compositions précédentes.

Prenons n = 4 comme exemple. On décompose 4 en somme de deux nombres. Il peut s'écrire : 3 + 1, 2 + 2, 1 + 3, ou [0+] 4 : on fait varier le dernier élément de la composition de 1 à 4 et l'on décompose l'élément de gauche à partir des compositions précédentes.

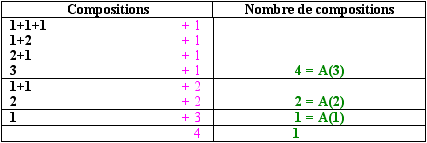
Cette méthode nous permet de conclure que :

[1]       A(4) = A(3)+A(2)+A(1)+1 = 8

I.3

Généralisons en décomposant n.

On fait varier le dernier élément de la composition de 1 à n, et on décompose l'élément de gauche selon les compositions précédentes.

[On en déduit la formule de récurrence (note 3) :]

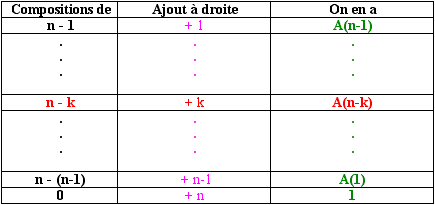
[2]       

D'après les exemples, on remarque les résultats suivants :

A(1) = 1 = 2⁰ ; A(2) = 2 = 2¹ ; A(3) = 4 = 2² ; A(4) = 8 = 2³ ou encore, A(5) = 16 = 2⁴.

Nous avons alors eu l'idée que A(n) pouvait s'écrire sous la forme d'une puissance de 2.

[... Nous pouvons] démontrer par récurrence que A(n) = 2^n-1 pour tout n. [Détail de la preuve].

[Théorème 1]    

Les partitions de n sont les suites d'entiers strictement positifs dont la somme vaut n, en ne considérant pas l'ordre des éléments de la suite. [Nous notons le nombre de partitions de l'entier n.]

II.1

[Nous pouvons maintenant donner une définition plus précise d'une partition : étant donné un entier n non nul, on appelle partition de n une suite croissante d'entiers non nuls dont la somme vaut n.]
Le nombre de partitions P( n) augmente très vite mais le lien qui pourrait exister entre les nombres de partitions n'est pas évident à déceler ([voir le] tableau de valeurs de A(n) et P(n)).
Essayons de trouver une formule qui nous permettrait de calculer le nombre de partitions d'un entier n. La base de nos recherches sera un article de Tangente sur les travaux d'Euler, Mac Mahon et Ramanujan.

II.2

[Conjecture 1 note 4]  [Formule de Mac Mahon : pour tout entier positif n, on a :]

(II.2.1)

- ... [Par convention, P(0) = 1 et un terme de la forme est nul dès que  n<r .]

La logique interne de la formule de récurrence ci-dessus ne saute pas aux yeux.

• [Les termes apparaissent par paires.] Une paire est définie par [de la forme] : .
• Les signes + et - changent alternativement devant chaque paire : +, puis -, puis +, puis - Š
• L'écart entre les deux valeurs r et q de la paire est de 1 pour la première, 2 pour la deuxième, Š, k pour la k-ième.
• L'écart entre le dernier [terme] de la k-ième paire et le premier de la ( k+1)-ième paire est de .

[Voici ce qu'on obtient avec ces règles :

	(Partie donnée par Tangente.)
	Partie vérifiée grâce aux valeurs de P(n) données par Tangente. [note 5]
- ...	Partie conjecturée.

Donc la forme de la k-ième paire serait : avec r à déterminer [en fonction de k; voir note 6].

II.3

Afin d'étudier les partitions, nous allons considérer la série génératrice des , c'est-à-dire un polynôme infini (note 7):

[autrement dit, en posant P(0) = 1 :]

Posons [note 8].

est donc un polynôme de degré infini, il s'écrit :

[...] l'égalité [s'écrit :]

Grâce au tableau de valeurs de A(n) et P(n), on obtient :

On développe ce produit et ainsi on a les coefficients de X⁰ , X¹ , X² , ... :

                   =

On identifie les coefficients :

	d'où
	d'où
	d'où
de même :
[et , en général : ]

Il semble que le coefficient a_k de X^k soit l'opposé du coefficient de P(n-k) dans la formule de récurrence de P(n) de Mac Mahon. [Voir § II.2]. Bref, on arrive à ...

[Conjecture 2] 

(II.3.1)

[formule] que nous avons vérifiée jusqu'à l'ordre 40.

II.4

Cherchons à factoriser cette série (note 9). Commençons par [mettre]   [en facteur] ce qui nous permet de faire disparaître le [terme en ] X dans la grande parenthèse [c'est à dire dans le second facteur]:

On fait de même avec (1-X²) ce qui, de même, permet de faire disparaître le [terme en ] X² dans la grande parenthèse [le second facteur]:

Nous continuons de même avec puis avec , etc. [ A chaque fois que l'on fait apparaître un facteur de la forme] , [on constate que le facteur complémentaire commence par ], Il semblerait donc que s'écrive sous la forme [...] :

[...] [Conjecture 3] Q(x) [défini par ] s'écrit sous la forme :

(II.4.1)

Cherchons à démontrer que pour cela redéveloppons Q(x) [ redéfinissons Q(x) par et évaluons(note 10)] :

est une somme infinie des termes d'une suite géométrique [donc] :

[note 11]

De même, on a :

Ainsi, [si la formule est vraie, on a :]

(II.4.2)

[..] [C'est le développement de cette expression factorisée qui va donner les coeficients de ]

II.5 [(note 12) ]

Lors du développement de , nous avons aperçu une correspondance entre le coefficient de Xⁿ , les partitions et le nombre P(n) :
quand [un terme] X^k.i intervient dans le développement de , on associera k.i à la somme de i termes égaux à k ; par exemple, 3.2 sera associé à 3+3.

[Expliquons les détails de cette correspondance en calculant le coefficient de X³][...]

[Rappellons les partitions de 3 : ]

3  =  1 + 1 + 1
    = 1 + 2
    =  3

[On a :]

[] =(1+X^1.1+X^1.2+X^1.3+X^1.4+...)(1+X^2.1+X^2.2+X^2.3+...)(1+X^3.1+X^3.2+ X^3.3+...)...

Pour obtenir X³, on peut prendre :

• X³ dans la première parenthèse donc pour nous X^1.3 puis des 1 dans les autres. X^1.3 est associé à 3 = 1 + 1 + 1.
• X dans la première parenthèse et X² dans la deuxième, ce qui s'écrit X^1.1 x X^2.1 , puis que des 1 dans les autres. X^1.1 x X^2.1 correspond à 3 = 1 + 2.
• X³ dans la troisième parenthèse soit X^3.1 [et 1 dans les autres]. Ceci correspond à 3 = 3.

De même pour X⁴ :

[] =(1+X^1.1+X^1.2+X^1.3+X^1.4+Š)(1+X^2.1+X^2.2+X^2x3+Š)(1+X^3.1+Š)(1+X^4.1+Š)Š

4  = 1 + 1 + 1 + 1
    = 1 + 1 + 2
    = 1 + 3
    = 2 + 2
    = 4

En appliquant cette méthode à tous les termes de F(X) [ de], nous pouvons déterminer le coefficient de Xⁿ, on retrouve P(n).

D'où

[] = 1+ X + 2 X² + 3 X³ + ... + P(n) Xⁿ + ...

[Théorème 2.    La série génératrice des nombres de partitions  satisfait à l'égalité suivante :]

Nous n'avons pas démontré les formules énoncées tout au long de cet exposé. Néanmoins le dernier résultat obtenu : l'égalité entre la série [génératrice F( X)] et le [produit infini] , valide les étapes intermédiaires. [note 13]

Comptes Rendus MATh.en.JEANS 99-10

© MATh.en.JEANS 2003. Tous droits réservés.

note 1. ... 150 ans de tradition horlogère, avec la technique du "décolletage"

retour à l'appel de cette note

note 2. Outre "les partitions d'entiers", deux autres sujets de Combinatoire étaient au menu : les différents pliages possibles des bandes de timbres et l'ordonnancement des piles de crêpes avec une pallette.
Le sujet des partitions d'entiers a été traité par d'autres ateliers de recherche "MATh.en.JEANS" : "Combinatoire autour du problème "007" (« Combien y a-t-il de décompositions d'un entier en somme d'entiers positifs rangés dans l'ordre croissant ? »), par F. Fournot et al., élèves des lycées Paul Éluard (93, St Denis) et Jacques Feyder (93, Épinay).

retour à l'appel de cette note

note 3. Lorsqu'une expression E( n) dépend d'un entier variable n, on appelle formule de récurrence (pour cette expression), une formule qui permet de déterminer la valeur de l'expression pour l'entier n à partir des valeurs précédentes (c'est à dire à partir des valeurs E( 0), E( 1), E( 2), ..., E( n-2) et E( n-1) ).

retour à l'appel de cette note

note 4. Les nombres 0,1,2,5,7,12,15,22,26,35,40,51,57,70,77, etc. qui apparaissent dans cette formule de récurrence sont connus sous le nom de nombres pentagonaux généralisés. Ce sont les nombres de la forme où m est un entier relatif quelconque. La formule était déjà connue d'Euler ("théorème pentagonal d'Euler"). Elle est ici prise par les auteurs comme une hypothèse de travail dont ils vont étudier les conséquences. Ils vérifient sa validité jusqu'à n=40.

retour à l'appel de cette note

note 5. Vérifions par exemple la valeur P(21). La formule donne : P(21) = P(20)+P(19)-P(16)-P(14)+P(9)+P(6), soit, (vu la table des valeurs de P(n)): P(21) =  627+ 490 - 231 - 135 + 30 + 11 = 792 ce qui est bien la valeur correcte.

retour à l'appel de cette note

note 6. Les différences successives des nombres q sont 4, 7, 10, 13, ... elles forment une progression arithmétique de raison 3. La valeur de r dans la k-ième paire de la formule est donc 1+4+7+10+...+(1+3( k-1)), ce qui s'écrit encore k+3(0+1+...+( k-1)). Le calcul classique de la somme des termes d'une progression arithmétique donne 0+1+...+( k-1)=k( k-1)/2. On en déduit une expression de la k-ième paire de la formule de Euler-Mac Mahon :
             

retour à l'appel de cette note

note 7. Une expression du type soit en abrégé est appelé une série formelle : elle résume toute l'information contenue dans la suite des coefficients P(0), P(1), P(2), P(3) ... sous la forme d'un "polynôme de degré infini". De telles sommes infinies furent systématiquement étudiées au XVIIIème siècle par le mathématicien suisse Leonhard Euler (1707-1783).

a) Séries formelles et troncatures.

Les séries formelles sont un outil combinatoire puissant permettant de traiter des suites de nombres. Leur mode d'écriture, calqué sur celui des polynômes, permet de généraliser les calculs avec les polynômes : le vocabulaire des polynômes et les règles usuelles pour l'addition et la multiplication s'étendent sans difficulté à ces polynômes "infinis", tout en offrant plus de possibilités.

Pour effectuer des calculs avec des séries formelles, on applique la règle des troncatures, en se servant des opérations usuelles sur les polynômes : pour calculer les k premiers termes du résultat, on ne retiendra de chaque série que sa troncature à l'ordre k, c'est à dire le polynôme formé des k premiers termes de la série : on effectue alors le calcul voulu sur ces polynômes et on ne retient du résultat que les termes de degré inférieurs à k.

En résumé :

la k-ième troncature du résulat cherché est la k-ième troncature du résultat calculé avec les k-ième troncatures.

En raison de la présence des termes constants (de degré 0), la troncature à l'ordre k d'une série formelle est un polynôme de degré au plus k-1 On l'appelera donc aussi troncature au degré (k-1).

Effectuons par exemple le produit (1 + 2X + 3X² + 4X³+ ...)(1 + X + X² + X³ + ...) :

b) Série formelle inverse d'un polynôme ou d'une autre série formelle.

La règle des troncatures montre que les séries formelles généralisent les polynômes : on peut identifier un polynôme A de degré k à la série formelle dont la troncature au degré k est A et dont les termes suivant sont nuls. Addition et multiplication de séries formelles héritent des propriétés de l'addition et de la multiplication de polynômes. Les séries formelles à coefficients entiers forment un anneau commutatif unitaire, que l'on note , avec pour unité la série formelle 1 + 0 + 0 + 0 + ...  que l'on note simplement 1. Plus généralement, on étudie les séries formelles où les coefficients sont pris dans un corps de nombres (nombres rationnels, réels, ou corps plus généraux) elles forment alors ce qu'on appelle une algèbre* commutative unitaire sur ce corps.

On peut se rendre compte de la puissance de cette généralisation en examinant le problème de la division : de même que les nombres rationnels permettent, en général, la division d'un entier par un entier (il suffit que le second entier, "le diviseur", ne soit pas 0), on peut démontrer que les séries formelles permettent en général la division d'un polynôme par un autre polynôme et même par une autre série formelle : il suffit que le terme constant de la seconde série formelle soit 1 ou -1.

Les auteurs révèlent l'explication de cette propriété dans la suite du paragraphe II.3, lorsqu'il évaluent les coefficients de la série formelle inverse de la série F(X). Donnons ici un exemple qui apparaîtra dans la suite de l'article.

Exemple : vous ne trouverez aucun polynôme qui multiplié par (1-X) donne 1. Alors que vous pouvez trouver facilement une série formelle qui multipliée par (1-X) donne 1 ! En effet, le produit (1+X+X²+X³+...)(1-X) vaut 1.1 + (1.(-X)+X.1) + (1.(0.X²)+X.(-X)+X2.(1))+... ce qui donne 1 + 0 + 0 + 0 + ... = 1 !

En résumé, la série formelle 1-X est inversible et a pour inverse la série formelle (1+X+X²+X³+...).

c) Sommes et produits infinis de séries formelles.

La règle de troncature permet également d'attribuer une signification à certaines sommes infinies ou à certains produits infinis de séries formelles :

• pour pouvoir calculer une somme infinie, il suffit que tout entier k satisfasse la condition suivante: les troncatures à l'ordre k des séries qui contribuent à la somme sont, à l'exception d'un nombre fini d'entre elles, nulles.
• pour pouvoir calculer un produit infini, il suffit que tout entier k satisfasse la condition suivante: les troncatures à l'ordre k des séries qui contribuent au produit sont, à l'exception d'un nombre fini d'entre elles, égales à 1. L'exemple : du produit infini (1-X)(1-X²)(1-X³).... est traité dans la suite de l'article.

retour à l'appel de cette note

note 8. Comme vont en fait le montrer les calculs qui suivent, la série formelle F(X), de terme constant 1, admet une série formelle inverse (voir note 7b), qui est Q(X),

retour à l'appel de cette note

note 9. Si B(X) est une série formelle inversible (voir note 7) et si A(X) est une série formelle quelconque, on peut toujours faire apparaître B(X) comme un facteur de A(X). En effet si B'(X) désigne la série inverse de B(X) on a :

A(X)= 1.A(X) = (B(X).B'(X)).A(X) = B(X).(B'(X).A(X))

On peut dire que le produit B'(X).A(X) représente le quotient de A(X) par B(X), autrement dit le résultat de "la division" de A(X) par B(X).

Ici les auteurs vont en fait mettre en oeuvre une autre technique de division, connue sous le nom de "division suivant les puissances croissantes" dont le principe est le suivant.

Division suivant les puissances croissantes. Si A(X) et B(X) sont des séries formelles, B(X) étant inversible, alors, il existe, pour tout entier k= 1, 2, 3, ..., un unique polynôme C_k(X) tel que les coefficients des k premiers termes de la série A(X)-B(X) C_k(X) soient nuls.

Autrement dit A(X) peut s'écrire sous la forme :

A(X) = B(X) C_k(X) + X^kR(X)

où R(X) est une autre série formelle.

Les C_k(X) constituent les troncatures à l'ordre k d'une unique série formelle C(X) qui vérifie A(X)=B(X)C(X).

retour à l'appel de cette note

note 10. Nous préférons faire apparaître dès maintenant la logique du raisonnement qui conduira au théorème 2 final, Ce raisonnement ne suppose pas que la conjecture 3 soit vraie : on prendcomme définition de la série formelle Q(X). Ce sont les coefficients de la série formelle inverse, qui vont être calculés,

retour au premier appel de cette note

note 11. Cette formule se vérifie aisément en multipliant la série formelle par la série formelle "géométrique"

retour à l'appel de cette note

note 12. Les auteurs avaient intitulé ce paragraphe "Coefficients de Q(X)" tout en travaillant avec l'expression, aussi écrite sous la forme F(X), (conformément à la conjecture 3). Nos changements respectent la logique démonstrative introduite dès la définition de Q(X) comme produit infini (cf. note 10).

retour à l'appel de cette note

note 13. Cette appréciation semble résolument optimiste et laisse pas mal de travail au lecteur. Rappelons que le présent texte est un compte rendu de l'exposé oral fait par les auteurs au 10ème congrès MATh.en.JEANS : il ne peut donc présenter toutes les démonstrations en détail.

Le raisonnement suivi dans le § II.5 établit le théorème 2, donc la conjecture 3 : l'égalité des séries F(X) et 1/Q(X) est obtenue en prouvant que quelque soit l'entier k, les coefficients de X^k sont les mêmes dans F(X) et 1/Q(X).

Pour souscrire à l'affirmation des auteurs et "valider les étapes intermédiaires", il reste à "remonter" les calculs et raisonnements des paragraphes précédents, et en particulier :

• voir que le produit infini se développe effectivement sous la forme (II.3.1) (Conjecture 2) ,
• voir que cette formule, grâce à la relation Q(X)F(X)=1 peut être réécrite sous la forme d'une relation de récurrence qui exprime P(n) en fonction des coefficients de la série Q(X) et des coefficients P(0), P(1), ..., P(n-1) de la série F(X).
• en déduire ensuite la formule de MacMahon-Euler (Conjecture 1).

retour à l'appel de cette note

nombre entier / somme / partition / partage / decomposition / nombre penagonal / tableau de young / serie generatrice /serie formelle / polynome / produit infini / division / puissances croissantes / suite geometrique / mac mahon / leonhard euler / combinatoire /ramanujan / recurrence /somme infinie / produit infini