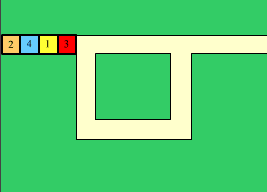
Exemple
procède avec
la situation "2413" ]
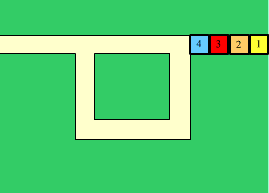
Marcel et ses wagons, Comptes Rendus MATh.en.JEANS 00-05
Marcel fait en réalité des math
En effet, les trains que Marcel doit ranger n'ont pas tous le même nombre de wagons, le nombre n de wagons peut donc varier ; ça ressemble étrangement à un problème de math.
Il faut aussi faire des math pour calculer le nombre de trains différents possibles avec un certain nombre de wagons.
Imaginons qu'on veuille créer un train de toutes pièces avec, par exemple, 3 wagons.
Un tel train a un wagon à gauche, un wagon au milieu, et un wagon à droite, en tout : 3 positions.
Le wagon 1 peut être placé à ces 3 positions.
Le wagon 2 peut être placé à 2 positions car le wagon 1 en occupe déjà une.
Le wagon 3 ne peut être placé qu'à 1 position car les wagons 1 et 2 en occupent déjà 2.
Récapitulons : 3 positions possibles pour le premier wagon puis, pour chacune d'elles, 2 positions différentes possibles pour le deuxième wagon, puis pour le troisième, une seule.
Le nombre de trains différents existant à trois wagons est donc :
Les voici :
On peut de la même façon généraliser et dire qu'il existe :
trains différents possédant n wagons.
La méthode de Marcel
Si on s'y prend mal, ranger un train peut devenir un vrai calvaire.
Heureusement, Marcel a trouvé une méthode qui permet de ranger un train " automatiquement " chaque fois que c'est possible.
- on stocke dans la dérivation les wagons à sa droite.
- on passe le wagon
1 par la voie principale.
|
|
Exemple procède avec la situation "2413" ] |

|
Cependant, même avec cette méthode, des trains ne peuvent être triés.
Pour 3 wagons :
132
213
231 sont triables.
312
321
Avec plus de wagons :
[on peut vérifier que :]
A 3 wagons : 5/6 sont triables A 4 wagons : 14/24 sont triables A 5 wagons : 42/120 sont triables A 6 wagons : 132/720 sont triables
Super : un critère !
Marcel, las de ses efforts vains à essayer de ranger des trains inrangeables a eu une idée astucieuse : il a trouvé un critère qui, sans même devoir manipuler un train, lui permet de dire si ce train est triable ou non.
Le critère : soient trois wagons numérotés a,b,c tels que a< b< c. S'ils apparaissent dans l'ordre suivant:
alors le train n'est pas triable.
Explication :

|
|
 |
|
  | |
  | |
|
 |
Exemple - Avec 14 wagons :
Les trois wagons en bleu suffisent à rendre le train impossible à ranger.
Marcel a une idée : le triangle
Pour avancer dans ses recherches, Marcel a eu l'idée de regrouper ses résultats sous la forme d'un triangle. Le voici :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Explications :
Ce triangle rassemble tous les résultats de 1 à 7 wagons, la 1ère colonne ceux pour 1 wagon, la 2ème colonne ceux pour 2 wagons ... la dernière colonne pour 7 wagons.
Ce triangle peut être poursuivi vers la droite ( n wagons ).
Prenons la 3ème colonne.
Il existe 6 trains différents à 3 wagons dont 5 sont triables avec la dérivation.
Parmi ces 5 trains, un seul commence par le wagon 1 (132), deux commencent par le wagon 2 (213 et 231), deux commencent par le wagon 3 (312 et 321).
La première ligne est constituée du nombre des trains triables commençant par le wagon 1.
La deuxième ligne est constituée du nombre des trains triables commençant par le wagon 2.
La n-ième ligne est constituée du nombre des trains triables commençant par le wagon n.
Ce triangle présente des
propriétés intéressantes en lien avec le
fameux triangle de
Pascal ![]()
La somme des nombres d'une colonne est le nombre total de trains triables comportant le nombre de wagons indiqué par la colonne.
On remarque que ce nombre se retrouve au sommet de la colonne suivante. [Par exemple la somme des termes de la colonne jaune est 14]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ainsi, le nombre Cn de trains triables à n wagons est égal au nombre de trains triables à (n+ 1) wagons commençant par le wagon [numéro] (n+ 1) mais aussi par le wagon numéro n ( les deux nombres en haut d'une colonne sont égaux ).
On retrouve ces résultats uniquement en manipulant les trains mais à vous de jouer.
Vous pouvez aussi démontrer que tout nombre de ce triangle est la somme du nombre à sa gauche et du nombre au-dessous de lui ... [exemple illustré avec les cases vertes]
Les propriétés de ce triangle nous permettent de le prolonger à l'infini vers la droite et connaître tous les résultats pour nos trains sans manipuler des milliers de wagons.
On trouve ainsi une formule
sympathique [...].
La Formule
Nous avons trouvé une formule (que nous n'avons malheureusement pas démontrée) et qui donne, en fonction du nombre n de wagons, le nombre Cn de trains triables par la dérivation.
|
|
C(n, k) désigne le
nombre de combinaisons |
Pour information, les nombres définis par
cette suite sont appelés nombres
de Catalan, ![]() du nom du
mathématicien belge qui les a découverts.
du nom du
mathématicien belge qui les a découverts.
MOTS
CLEFS
COMBINATOIRE ENUMÉRATIVE PERMUTATION COEFFICIENTS BINOMIAUX NOMBRES DE CATALAN TRI WAGONS
|
Comptes Rendus MATh.en.JEANS 00-05 |
© MATh.en.JEANS 2001. Tous droits réservés. |