[Article vérifié et commenté
: les passages entre crochets sont des éditeurs]
Comptes Rendus MATh.en.JEANS 01-01
Jumelage
MATh.en.JEANS entre les lycées d'altitude de
Briançon (05) (Atelier Scientifique et Action "Passion
Recherche") et Jean Moulin de Pézenas (34), année
scolaire 2000-01.
Enseignants : Hubert PROAL (Briançon),
avec la participation de Luc SAVIGNEUX (Pézenas)
Chercheur
(correspondant) : Patric VEROVIC
[Article vérifié et commenté
: les passages entre crochets sont des éditeurs]
I) Présentation générale du problème
On trouve dans de nombreuses machines des systèmes d'engrenages destinés à multiplier ou à démultiplier une vitesse d'entrée pour obtenir une vitesse de sortie bien particulière.
Les exemples sont nombreux, comme les boites de vitesse de nos voitures, ou encore les engrenages des montres et des horloges.
Nous disposons d'un arbre tournant à une vitesse angulaire W. A la sortie on veut une vitesse angulaire k.W où k=0,23 (par exemple).
Il faut donc essayer de trouver une méthode générale pour placer des engrenages (dont on définira le plus petit et le plus grand), qui ont par exemple entre 15 et 50 dents pour obtenir le rapport k.
a) Historique
Les premières machines construites afin de modifier des vitesses angulaires étaient des roues de friction.
Ces roues étaient lisses et construites dans un matière qui avaient un fort coefficient de frottement.
Elles étaient maintenues en pression l'une contre l'autre, et le frottement qui se créait entre ces deux roues assurait la rotation des roues.
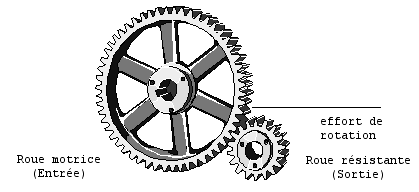
Mais ce système ne permettait pas de contrôler correctement le rapport k qui existait entre les vitesses angulaires d'entrée et de sortie. En effet les frottements qui existaient entre les roues n'étaient pas constants et le rapport k variait lui aussi.
D'où l'idée de mettre autour de la roue des " obstacles ", des dents pour augmenter la précision de la transmission de l'effort entre les roues.
Ainsi naissent les engrenages dotés de dents et qui permettent d'obtenir des rapports de transmission très précis.
b) Etude du rapport de transmission dans un couple d'engrenages
On appelle couple d'engrenages un montage constitué d'un pignon moteur denté et d'une roue réceptrice, elle aussi dentée.
Notations pour une roue d'engrenage:
On appelle W sa vitesse angulaire.
On appelle D son diamètre.
On appelle Z son nombre de dents.
On appelle p le pas de la denture.
Aux notations sont associés des indices qui les lient aux roues auxquelles elles se rapportent.
Par exemple W2 correspond à la vitesse angulaire de la roue 2, Z25 le nombre de dents de la roue 25 etc....
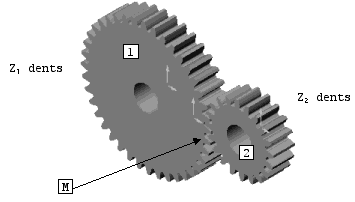
Pour engrener les 2 roues d'un engrenage doivent avoir le même pas.
On a la relation qui lie la circonférence et le pas p D= Z.p
donc p= p D/Z
or p1=p2
donc 
et donc 
.
Au point M les extrémités des 2 dents ont la même vitesse linéaire (et non pas angulaire).
On a la relation 
(relation liant
la vitesse avec la vitesse angulaire en fonction du rayon qui est la moitié
du diamètre) ; donc
On obtient la relation 
d'où on déduit que W1.Z1=W2.Z2
Par définition, le rapport d'un montage d'engrenage est égal au quotient de la vitesse angulaire de sortie par la vitesse angulaire d'entrée.
Ce rapport est aussi égal au rapport inverse du nombre de dents des roues.
Soit k ce rapport de réduction alors :
|
Remarques: - On voit bien ici le rapport inverse du nombre de dents par rapport aux vitesses de rotation (inversion des indices). - Il est important de considérer un rapport de réduction
sous forme fractionnaire comme une chose qui existe. Ainsi si |
donc 
.
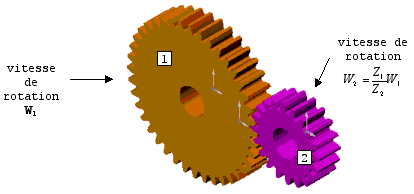
Nous voici désormais en possession de la formule de base des engrenages.
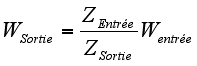
c) Etude des rapports de transmissions avec plusieurs couples d'engrenages
|
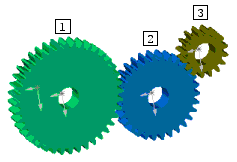
D'après la formule précédente on a: on a aussi: Si on remplace Z2 par sa valeur on a: |
On démontre facilement par récurrence [sur le nombre de roues] que les roues intermédiaires situées entre l'entrée et la sortie n'ont aucune influence sur le rapport de réduction du montage et ce quelque soit leur place et leur nombre.
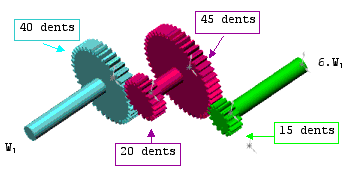
Par exemple pour le montage suivant, les roues intervenant dans le rapport de réduction sont la 1 et la 6 seulement.
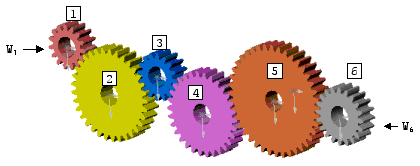
On a la relation 
.
Les roues intermédiaires n'ont aucune influence sur le rapport de réduction. Le rapport ne dépend alors que du nombre de dents des roues d'entrée et de sortie. On n'aura donc qu'un nombre limité de rapports de réduction possibles et pas nécessairement ceux désirés. Par exemple si on veut réaliser le rapport 6, il faut trouver 2 roues dont le quotient des nombres de dents vaut 6. Or dans notre intervalle [15 , 50] on ne dispose pas des roues nécessaires.
6 n'étant après tout pas réellement difficile à faire [car c'est un petit nombre entier ?], on imagine assez bien que des rapports du type 0.28 ou 3.15478 sont irréalisables avec cette méthode.
Il faut donc imaginer une astuce pour élargir nos possibilités.
d) Les arbres
|
Si on utilise un arbre pour relier 2 roues on garde la même vitesse angulaire pour un nombre de dents différents.
|
|
Etude d'un montage de 4 roues avec 2 arbres
|
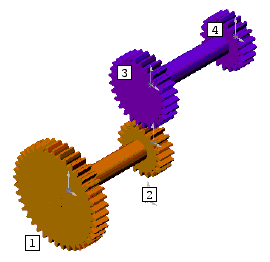
On cherche W4 en fonction de W1 On a On s'aperçoit que le rapport de réduction de ce montage correspond au rapport des roues qui se touchent directement.
|
Montons plusieurs roues avec des arbres et étudions ce qui se passe.
|
|
On a les relations donc On voit ici que le rapport de réduction de ce montage ( |
Par récurrence on démontre que le rapport total d'un montage du type précédent est égal au produit des rapports des montages intermédiaires (roues qui se touchent directement).
On a maintenant la relation suivante pour un montage avec n roues:
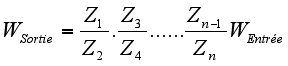
On voit maintenant que si le rapport que l'on veut réaliser est compliqué il suffira de le décomposer en pleins de petits rapports simples à réaliser.
6 qui était infaisable tout à l'heure est désormais réalisable :
. Il suffit de monter en série deux montages ayant pour rapport
2 et 3 ce qui est très réalisable.
suite :
III) Analyse mathématique
|
Comptes Rendus MATh.en.JEANS 01-01 |
© MATh.en.JEANS 2001. Tous droits réservés. |
il s'agit du rapport de réduction formé par
une roue de 47 dents et une roue de 23 dents.
.
.
.
) est égal
au produit des rapports des roues qui se touchent directement.